全部分类/
中学教育/
中学数学·初中版

中学数学·初中版

2024年04期

扫码免费借阅

目录

快速导航

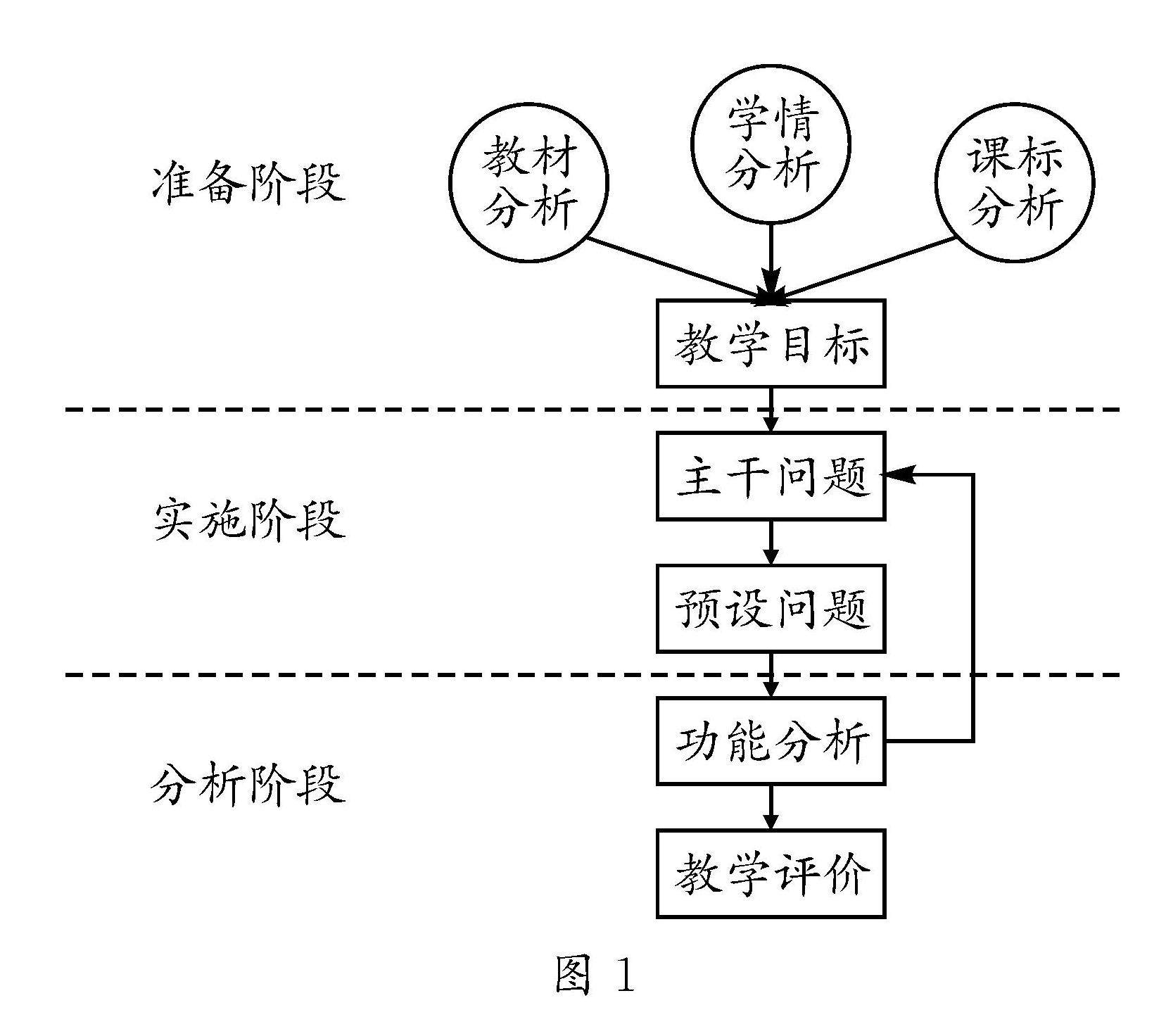
教法探索 | 基于问题链的单元复习教学策略研究

教法探索 | 基于问题链的单元复习教学策略研究

课题信息：安徽省合肥市教育科学研究一般课题“初中数学几何思维可视化教学实践研究”，课题编号为HJG22055. 摘要：复习课是初中阶段的主要课型之一，但由于缺乏系统的理论指导，使得复习课缺乏设计，变得低效，而运用问题链教学法可以帮助学生厘清知识脉络，树立整体观念，提高课堂参与度，发展数学核心素养.本文中给出了基于问题链的设计路径与设计原则，并以“直线与圆的位置关系”单元复习为例展开教学过程，为一
教法探索 | 做数学行推理

教法探索 | 做数学行推理

课题信息：南京市“十四五”规划课题2021年度重点课题“‘做数学’理念下初中生逻辑推理素养的实践研究”，课题编号为LZD/2021/17. 摘要：“做数学”对初中学生逻辑推理能力素养的培育至关重要.基于教学案例，分析“做数学”的教学价值，“做数学”理念下的新课堂应当普及并推广.以“做”为支架，革新课堂设计策略，“先做后学”可以更好地促进学生全面发展. 关键词：“做数学”；逻辑推理；教学案例；教
教法探索 | 优化运算策略培养运算能力

教法探索 | 优化运算策略培养运算能力

课题信息：教育部福建师范大学基础教育课程研究中心2023年度开放课题“新课程背景下初中数学课前教学质量评价研究”，课题编号为KCA2023340；福建省教育科学“十四五”规划2022年度课题“新课程背景下初中数学课堂教学质量评价研究”，课题编号为FJJKZX22-439. 摘要：挖掘图形特征是解几何题的关键，选择合理的运算策略，能够促进学生几何直观、抽象能力和推理能力的发展，是培养学生数学关键能
教法探索 | 基于深度学习的“相似变换运动轨迹”课堂设计

教法探索 | 基于深度学习的“相似变换运动轨迹”课堂设计

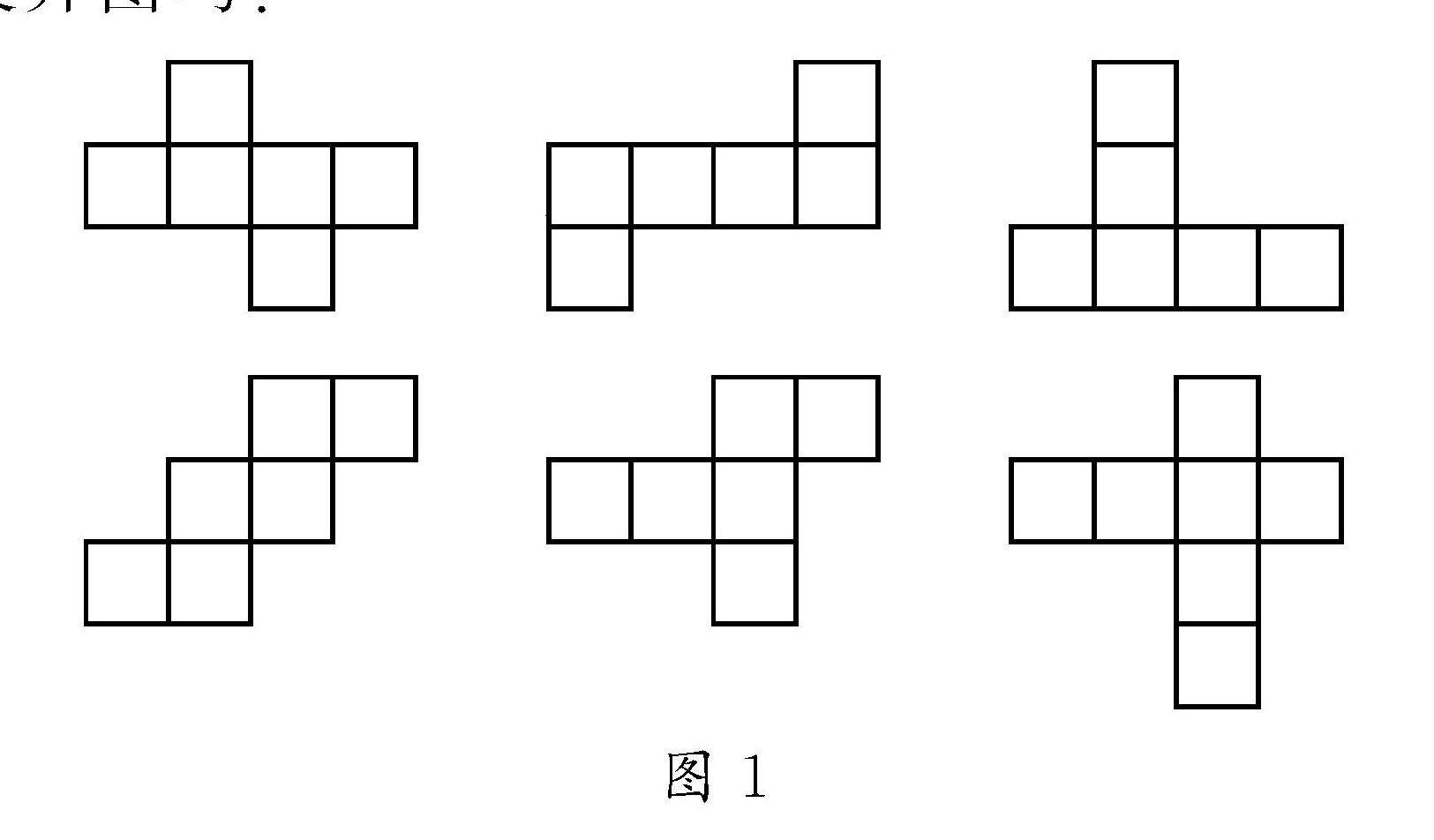
项目信息：广州市教学成果培育项目（Guangzhou teaching achievement cultivation project）“指向深度学习知识可视化原理的初中数学混合式教学的研究与实践”，项目编号为2023128470. 摘要：初中数学深度学习的教学设计重点在于通过精心设计问题情境和学习任务，引发学生认知冲突和深度思考.基于深度学习的“相似变换运动轨迹”课堂设计，引领学生经历问题情境
教法探索 | 初中阶段发展学生空间观念的五种路径

教法探索 | 初中阶段发展学生空间观念的五种路径

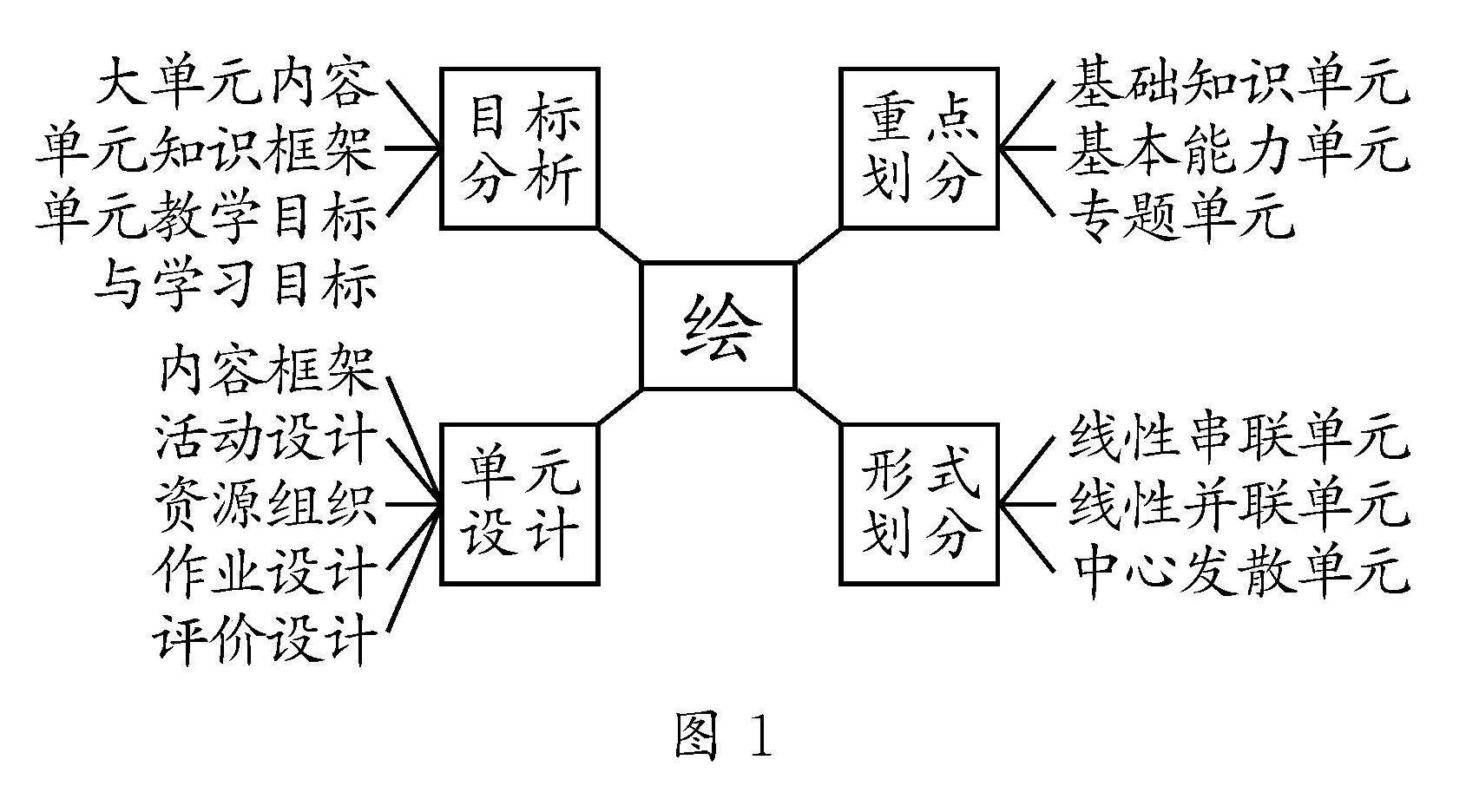
项目信息：广东省教育科研“十三五”规划2019年度教育科研一般项目“初中生数学核心素养测评研究”，课题批准号为2019YQJK349；中山市教育科研2020年度重点立项课题“‘至简数学’的理论与实践研究”，课题编号为A2020019. 《义务教育数学课程标准（2022年版）》指出“空间观念”主要是指对空间物体或图形的形状、大小及位置关系的认识.具体包括：（1）能够根据物体特征抽象出几何图形，根据
教法探索 | 绘·炼·驱·拓：多维数学思维品质的提升策略研究

教法探索 | 绘·炼·驱·拓：多维数学思维品质的提升策略研究

摘要：本文中以“一次函数”复习教学为例，分析了基于大单元整体设计，将知识点有机结合起来，构建完善的知识体系.通过“把控”全局、大单元划分、设计单元学习活动等策略激发学生的学习兴趣，提升多维数学思维品质，提高学生数学核心素养. 关键词：大单元；整体设计；数学思维《义务教育数学课程标准（2022年版）》指出，数学课程要培养的学生核心素养，主要指“三会”.其中“会用数学的思维思考现实世界”强调：培
教法探索 | 核心素养下初中数学单元整体教学有效性探究

教法探索 | 核心素养下初中数学单元整体教学有效性探究

摘要：以“平行四边形”和“特殊平行四边形”教学为例，将单元知识整合起来，寻找各个重难点实施教学，通过确定单元整体目标、借助知识迁移构建完整结构、明确各个单元逻辑关系、实施创新型作业设计等策略进行单元整体教学，帮助学生掌握知识、提高学习能力，进而培养核心素养. 关键词：核心素养；单元整体教学；有效性数学核心素养是数学课程目标的集中体现，是在数学学习和应用的过程中逐步形成和发展的［1］.核心素养
教法探索 | 问题法驱动下“相似三角形的判定”教学活动的实践

教法探索 | 问题法驱动下“相似三角形的判定”教学活动的实践

摘要：问题是认识世界和改造世界的原始动力，数学科目也不例外.本文中以“相似三角形的判定”一课的教学设计为例，结合问题法应用的两个原则，从“在现实情境中发现数学问题”和“利用新旧知识间的联系生成和解决问题”这两个方面探讨了在数学单元教学活动中运用问题法的实践和探索. 关键词：问题法；相似三角形的判定；教学实践问题是认识世界和改造世界的原始动力，数学学科也不例外.克莱因强调：“每一个数学分支均是
教法探索 | 运用变式教学促进深度学习

教法探索 | 运用变式教学促进深度学习

1 问题呈现例1 如图1所示，在正方形ABCD中，G是BC边上的任意一点，DE⊥AG，垂足为E，BF∥DE，且交AG于点F. 求证：AF－BF=EF. 例1是“正方形”一课的课后习题，该题是一道典型习题，涉及的知识点较多，可以很好地考查学生知识的迁移、重组能力，促使学生直观想象和逻辑推理等素养的提升. 八年级的学生已经拥有一定的知识储备，具有一定的分析和解决问题的能力，也具有一定的逻辑
教法探索 | 借“问题链”深度思考

教法探索 | 借“问题链”深度思考

摘要：以“问题链”为主线串联数学课堂，不仅可以展示最真实的数学课堂，助力精彩课堂的演绎，还能促进有质量的深度思考，潜移默化地发展学生的数学素养.文章阐释了“问题链”的价值解读，探寻“问题链”的实施路径，并对设计“问题链”提出了几点思考. 关键词：问题链；深度思考；课堂教学初中生处于思维高速发展时期，也就是心理学家皮亚杰所述的“形式运演阶段”，因此需要教师在引导学生获取知识技能的同时能促进学生
教法探索 | 以“认知冲突”促成“概念生成”

教法探索 | 以“认知冲突”促成“概念生成”

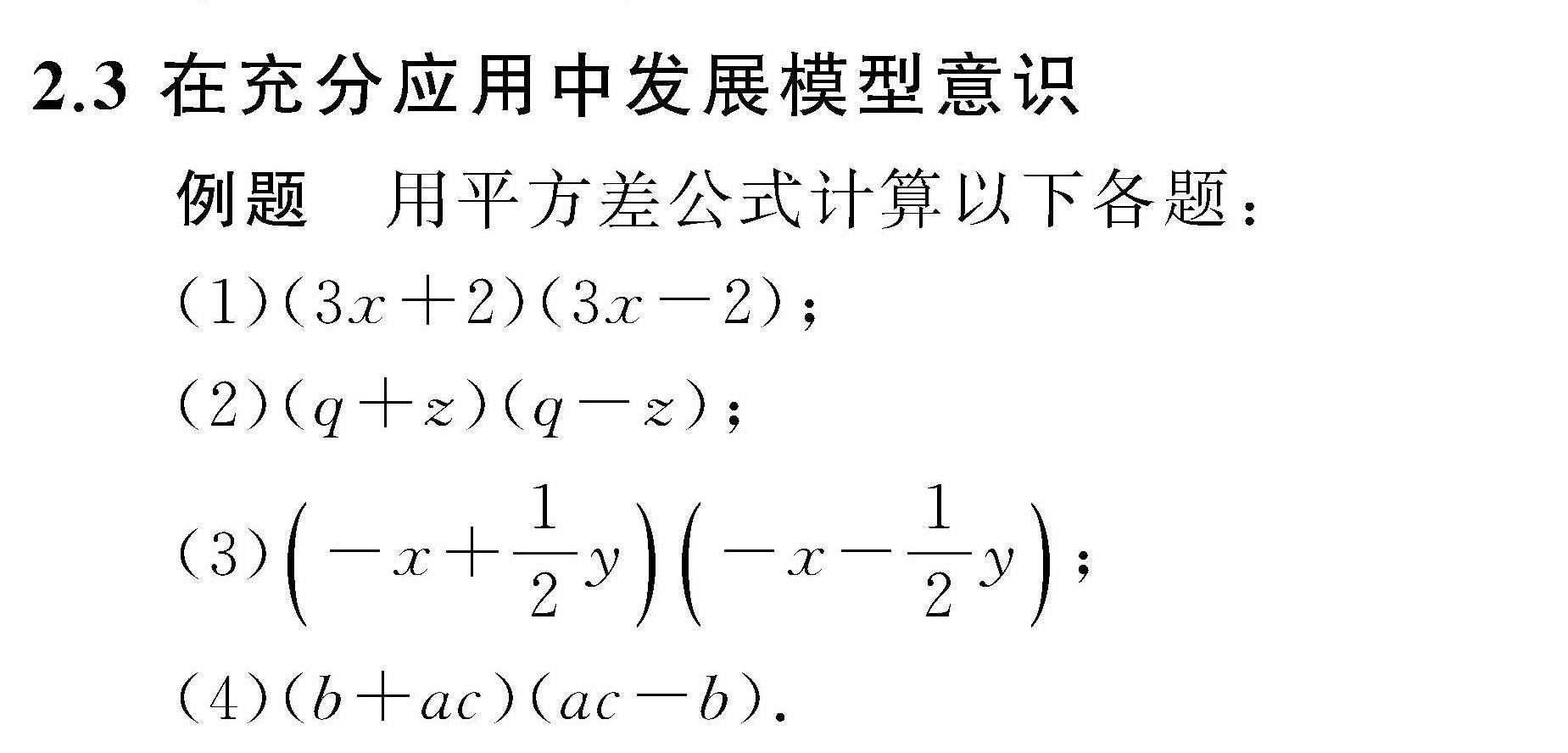
摘要：加权平均数是描述数据集中趋势的一种定性表达形式，“加权平均数”的教学价值重在创设真实的统计情境，促成加权平均数概念的生成，彰显学生在统计内容的学科素养发展，实现加权平均数的教育价值. 关键词：“权”概念的生成；“权”的价值；案例教学 1 教学价值分析 1.1 课标价值统计学是一门关于收集、整理和分析数据的方法论科学，其目的是探索数据内在的数量规律为制定决策提供依据.统计与其他数学内
教法探索 | 基于数学核心素养的公式教学

教法探索 | 基于数学核心素养的公式教学

当前，课程改革由能力立意体系朝着素养立意体系转变，数学核心素养已然成为各学段数学课程育人的核心任务及目标.那么，在初中数学课堂教学中该如何具体落实核心素养的培养呢？史宁中教授基于核心素养曾描绘过这样一个理想的教学过程：从知识本质出发，牢牢把握学生的认知，以问题为载体创设适切的教学情境，启发学生的数学思维，引发合作探究，从而使学生在自主获得知识技能的同时切实领悟知识本质，感悟数学思想，以实现数学核心
教法探索 | 借助单元整体结构化教学，促进学生深度学习

教法探索 | 借助单元整体结构化教学，促进学生深度学习

摘要：教师要创新教学方法，从学生本位出发采用单元整体结构化教学，才能让学生自主获取知识技能，发展数学核心素养.本文中以“一元一次方程”为例，从单元整体结构化教学的角度着手探讨促进深度学习的策略，并提出在深度探究中获取研究思路，在深度体验中实现整体建构，在迁移运用中领悟章节价值. 关键词：整体结构化教学；深度学习；一元一次方程新课程改革深化的当前，教育形态呈现了巨大的变化，随之出现了不少新的教
教法探索 | 基于“三会”的课堂教学设计与思考

教法探索 | 基于“三会”的课堂教学设计与思考

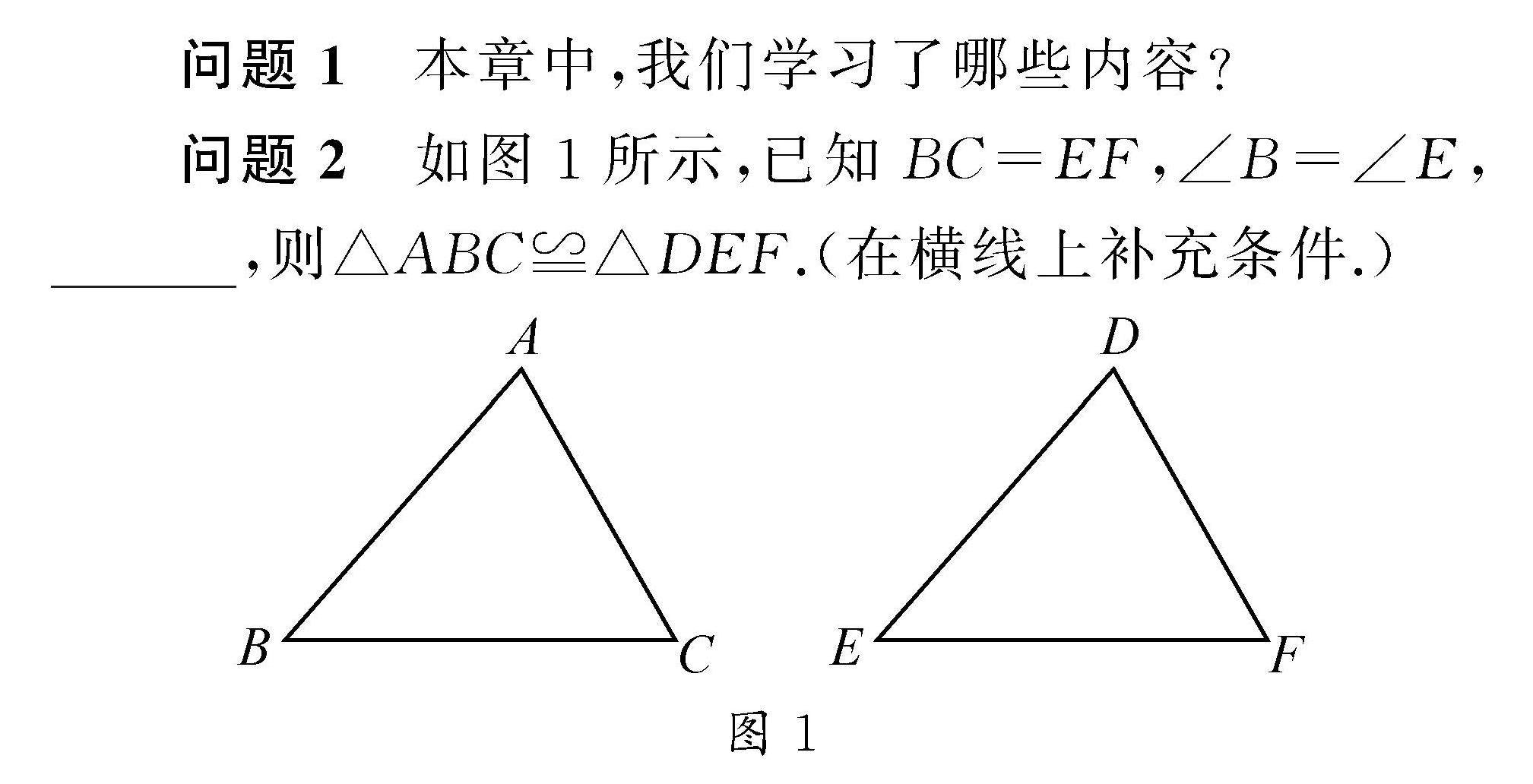
摘要：以“平方差公式”教学设计为例，从教学设计、教学理解、教学活动三方面，谈基于“三会”的课堂教学设计与思考. 关键词：“平方差公式”;“三会”;教学设计与思考 “三会”即会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界.那么，这些素养要求在课时教学中该如何具体落实呢？下面以“平方差公式”这节课为例，谈谈基于”三会”的课堂教学设计与思考. 1 教学分析本
教法探索 | 指向思维提升的初中数学单元复习课教学设计的实践

教法探索 | 指向思维提升的初中数学单元复习课教学设计的实践

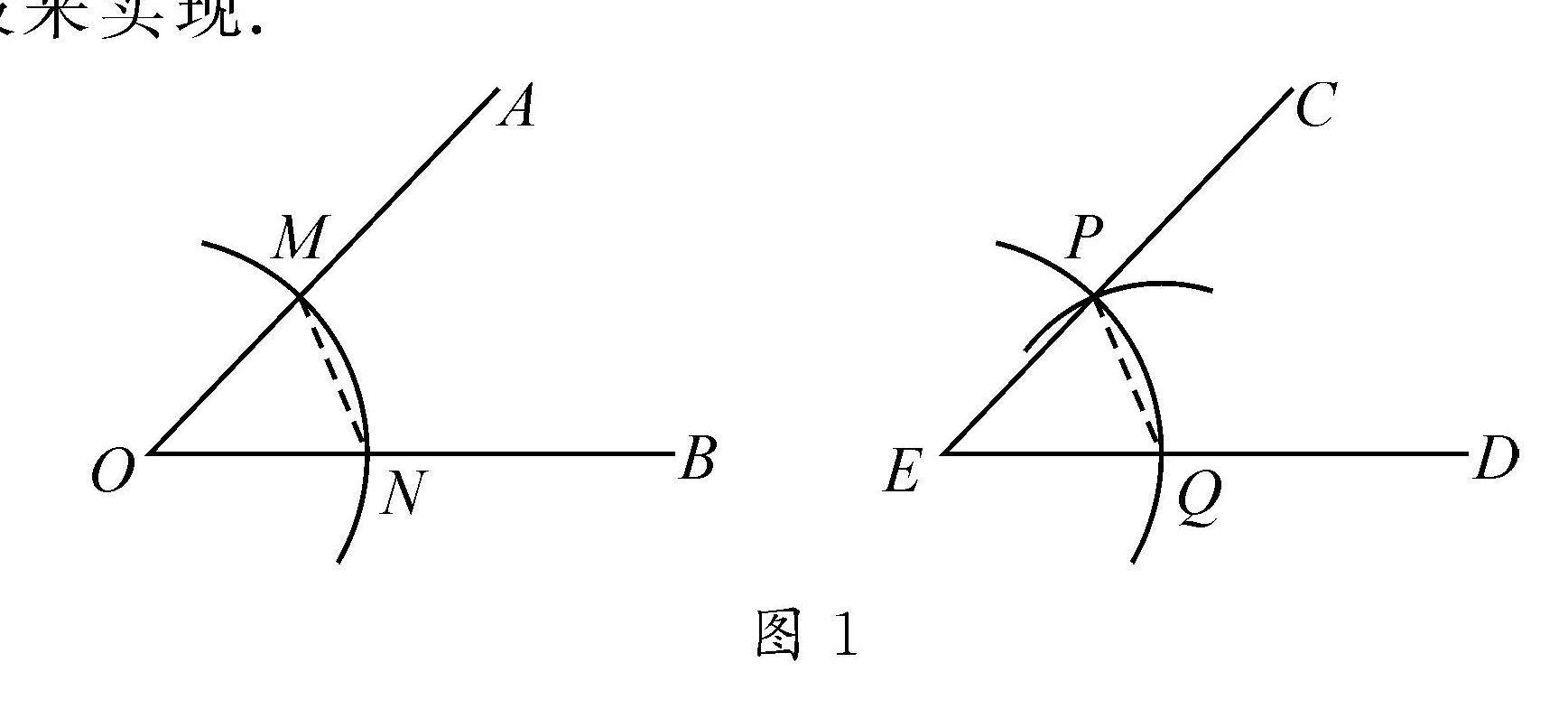
课题信息：盐城市教育科学“十四五”规划2021年度课题“基于PBL模式的初中数学单元教学案例研究”，课题编号为2021-L-204. 传统教学中的理解和识记知识已经无法适应当前新课程改革理念下的数学教学目标，而是需要教师将培养学生思维能力和创新能力等作为教学的主要任务.这就要求教师在设计教学时以提高思维能力为指导，以培养理性思维习惯和能力为目的，突出数学主线，凸显知识的内在逻辑联系与思想方法，落
教法探索 | 找准问题方向挖掘问题本质

教法探索 | 找准问题方向挖掘问题本质

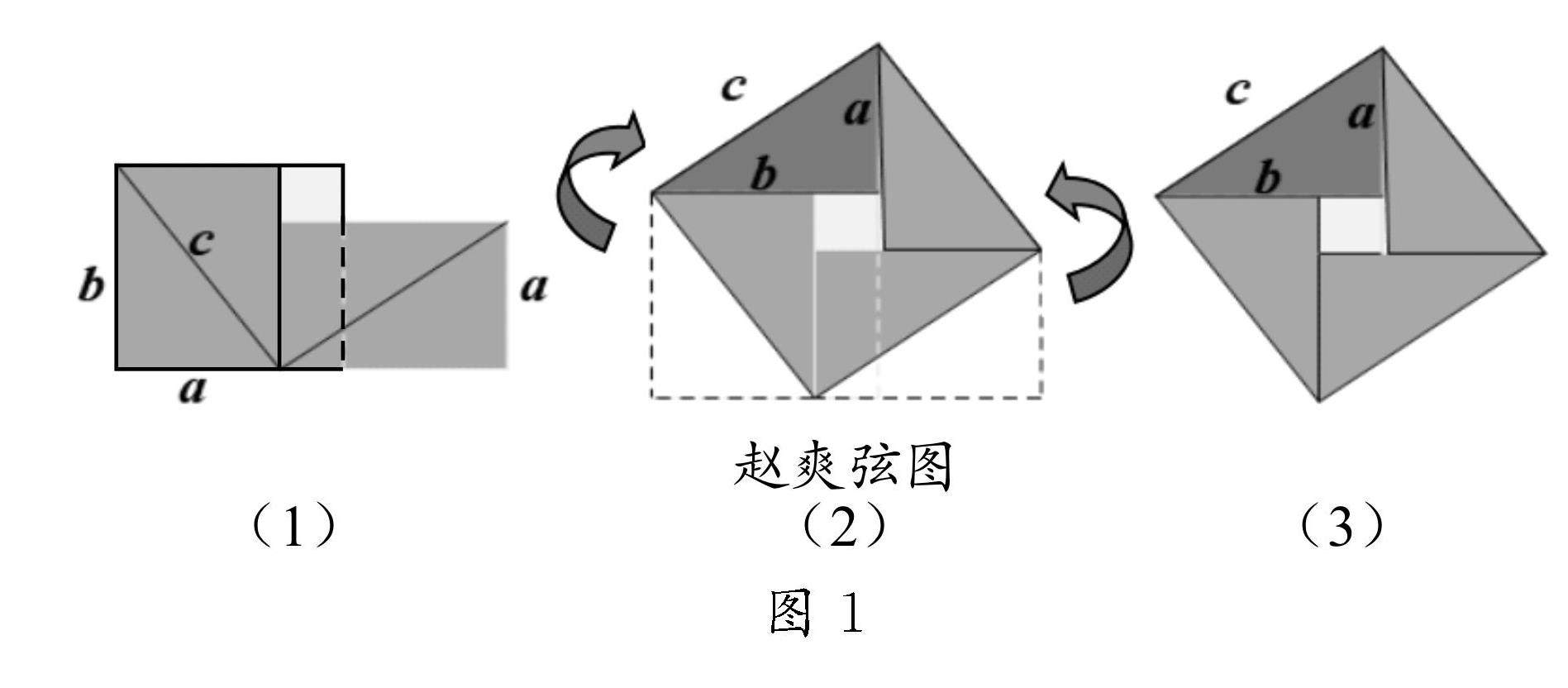
1 教学背景 1.1 教学分析在本课教学前，学生已经学习了用尺规作线段、作角的基本方法，具备一定的操作经验.不过以上基本作图的方法分散于不同的章节，影响知识的系统化建构，使得学生综合运用知识的能力还比较欠缺.另外，因受“讲授式”教学模式的影响，学生作图时大多依赖于模仿，对“为什么这样做”的理解还不够深入.在本节课中，教师从学生已有经验出发，带领学生深度挖掘问题的本质，让学生在掌握尺规作图基本
学生学习 | 基于数学核心素养的“勾股定理”教学实践研究

学生学习 | 基于数学核心素养的“勾股定理”教学实践研究

摘要：学生经历探索和证明勾股定理的过程，发展抽象、几何直观素养；通过归纳、猜想、验证培养逻辑推理能力；通过动手操作画图、拼图等活动培养直观想象能力、创新思维，落实数学核心素养培养. 关键词：数学核心素养；勾股定理；课堂教学培养初中学生的数学核心素养，就是要培养学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界.在义务教育阶段，数学眼光主要表现为抽象能力（数
学生学习 | 渗透数学思想方法提升学生数学素养

学生学习 | 渗透数学思想方法提升学生数学素养

圆周角、圆周角定理及其推论是解决圆内有关角的问题的基础，并为后续学习圆的内接四边形的角的关系提供前提，是初中数学的重要内容之一.在学习本课内容前，学生已经理解并掌握了圆的基本概念，本课是对圆周角的度数及其所对弧的度数关系的深入探究.在本课教学中，教师从学生已有知识和已有经验出发，为学生搭建平等、和谐的自主探究环境，并在“有形”的定理证明中渗透“无形”的数学思想方法，让学生充分感知数学思想方法的价值
学生学习 | 高阶思维在初中数学课堂中的生成策略

学生学习 | 高阶思维在初中数学课堂中的生成策略

摘要：追求高阶思维课堂不仅可以提高教育教学的质量，还能培养创新人才，更重要的是可以发展学生的数学核心素养.文章以“解一元二次方程（配方法2）”的教学为例，阐述了发展高阶思维能力的实践，并提出教师需深挖教材内容，设计优质问题，充分让学引思，重视总结提炼，提高高阶思维能力. 关键词：高阶思维；一元二次方程；配方法追求高阶思维课堂不仅可以提高教育教学的质量，还能培养创新人才，更重要的是可以发展学生
学生学习 | 经历推理过程，培养代数推理能力

学生学习 | 经历推理过程，培养代数推理能力

摘要：将推理能力的培养任务交给几何是不当的，教师应充分挖掘代数中的推理素材，让学生经历推理的过程，以培养学生的代数推理能力.文章以一节“等式的基本性质的应用”的研究课为例进行了一次尝试，让学生感受推理过程，积累推理经验，提升核心素养. 关键词：代数推理；等式的基本性质；课堂教学作为数学基本思维方式之一，推理对于人们的学习与生活具有十分重要的意义和价值.《义务教育数学课程标准（2011年版）》
学生学习 | 中考数学探索性问题答题策略

学生学习 | 中考数学探索性问题答题策略

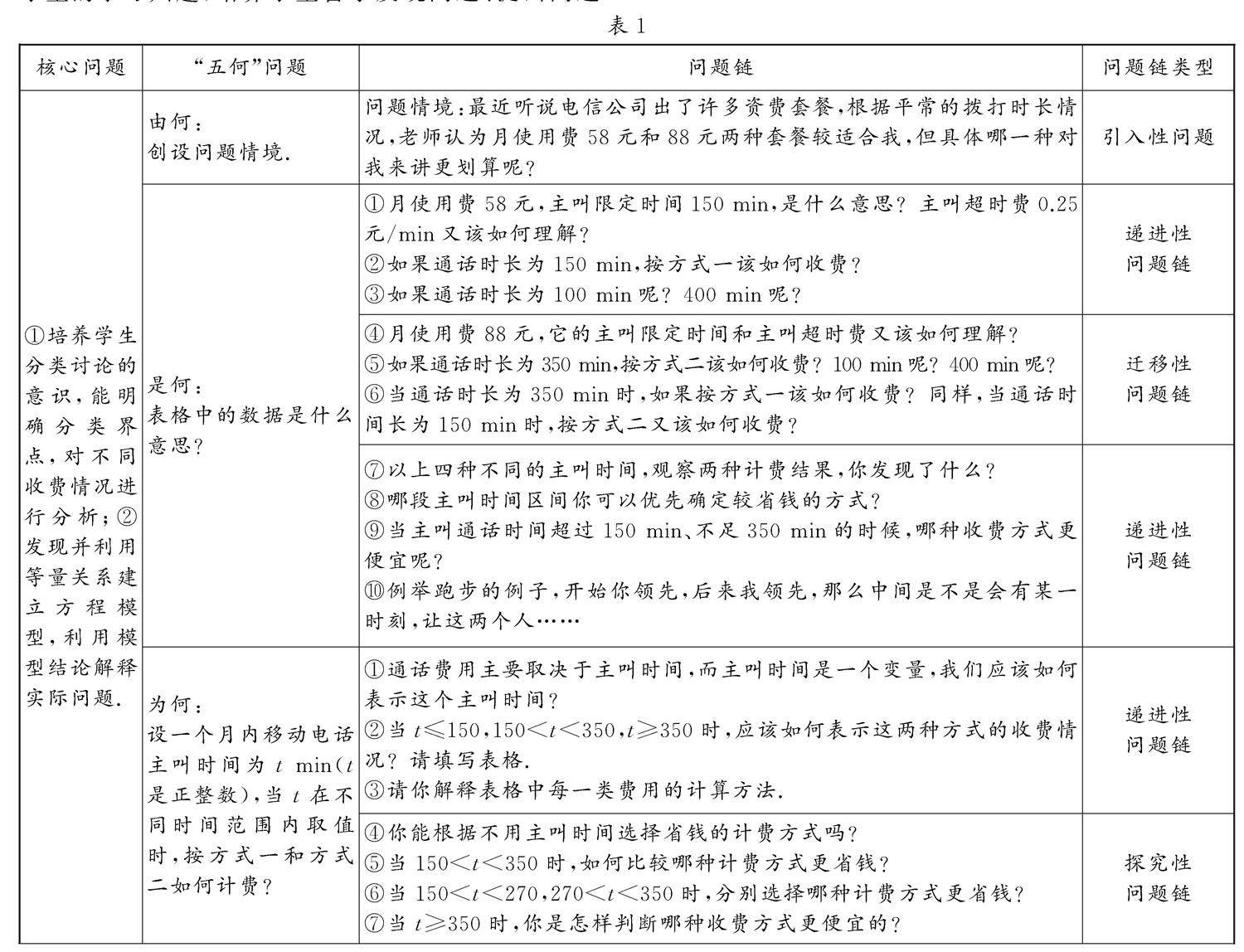
摘要：数学探索是一种重要的研究问题、解决问题的方法，也是人们探索和发现新知识的重要手段，有利于培养和发展创造思维能力.探索性问题已成为近年来中考数学的热点题型，本文中结合中考真题，对常见的几种探索性问题进行了归类、整合与解析，帮助学生熟悉探索性问题的答题策略，掌握解答的方法与技巧. 关键词：规律探索型；条件探索型；结论探索型；存在性探索型；尝试性解答初中数学课程标准要求教师“引导学生通过实践
学生学习 | 以问题为导向的初中数学深度学习初探

学生学习 | 以问题为导向的初中数学深度学习初探

摘要：以问题为导向的初中数学教学是促进学生深度学习的一个重要途径，以问题驱动学生主动参与、具身探究，形成高阶思维、创新能力等综合素养，真正体现了学生学习的主体地位.本文中以“电话计费问题”为例，将以问题为导向的教学策略研究与深度学习有机结合，为初中数学教育教学研究打开新格局. 关键词：初中数学；深度学习；问题；思维 2021年，教育部推动“双减”政策全面落地，如何在“减”量的背景下实现“增”质
学生学习 | 挖掘特征寻突破巧解压轴促创新

学生学习 | 挖掘特征寻突破巧解压轴促创新

摘要：近几年来一些地区中考数学压轴试题中所考查的几何图形问题，相对来说都比较难，解题过程中思路有时候一下子难以抓到，因此加强问题“特征”研究，结合相应方法进一步探究具体的思路，能快速抓住问题本质，让问题得到化解.本文中从“最值”“特殊角”“模型”和“规律”等方面作简单说明，以便取得化难为易的效果，从而更好地激发学生的创新思维. 关键词：问题特征；突破；中考压轴；创新数学变换方法是研究和解决数
学生学习 | 从“灵魂三问”谈自学能力的培养

学生学习 | 从“灵魂三问”谈自学能力的培养

摘要：随着“双减”政策的推广以及核心素养培养的研究越发深入，各地中考试题的命题也越发灵活，特别是笔者所在地区的“新定义”试题对材料的理解能力要求越来越高.学校在日常教学管理中也在逐渐加大数学核心能力的培养，其中对于学生自学能力的要求也逐渐提升.如何进行有效自学？本文中给出了在平时的教学中运用“三问”法进行自学能力培养的策略，进而提升学生的学习能力与学习效率. 关键词：“三问”法；自学；自学能力；
评价透视 | “双减”背景下初中数学作业设计的策略

评价透视 | “双减”背景下初中数学作业设计的策略

课题信息：江苏省教育学会“十四五”教育科研规划一般课题“‘双减’背景下初中生数学个性化作业设计研究”，课题编号为22A06SXLYG408. 摘要：“双减”即减轻义务教育阶段学生的作业负担和校外培训负担，每一位教师都要积极地响应这一政策，能够从多个角度出发开展作业设计，为学生带来全新的学习体验.本研究通过实践，对有效设计初中数学作业的策略进行了探索. 关键词：“双减”；核心素养；作业设计 2
评价透视 | 减而不简，作业何必是作业

评价透视 | 减而不简，作业何必是作业

课题信息：江苏省南京市教育科学“十四五”规划课题“素养为本的初中数学融合作业整体设计与实施研究”，课题立项号为L/2021/249. ——以苏科版“一次函数”单元复习作业设计为例在《义务教育数学课程标准（2022年版）》的指引下，数学作业设计应打破“课后作业”，重构“学程作业”，打破“统一作业”，重构“梯度作业”，打破“单一作业”，重构“多元作业”，让作业减而不简，夯实“四基”，培养“四能”
评价透视 | 考查基本能力，重视核心素养

评价透视 | 考查基本能力，重视核心素养

摘要：近几年的武汉中考试题板块之间相对保持稳定，适当创新，非常契合新课程标准理念.2023年的中考试题关注到了对学生基本能力的全面考查，充分重视数学核心素养的考查.本文中摘选了2023年中考试卷中的几道典型试题进行赏析. 关键词：基本能力;核心素养;试题赏析 1 考查理解能力，重视数学抽象试题1 （试卷第10题）皮克定理是格点几何学中的一个重要定理，它揭示了以格点为顶点的多边形的面积S＝
解题天地 | 二次函数综合性题目的解题方法研究

解题天地 | 二次函数综合性题目的解题方法研究

摘要：二次函数的综合性问题是中考数学试题的必考题型，可以系统地考查学生的数学建模能力和抽象思维能力.在求解过程中，能促使学生将离散化的知识聚合成统一的知识体系，同时能培养和发展学生解决实际问题的数学能力.文章结合具体例题分类探讨了二次函数综合题中的交点问题、线段的和差最值问题、一般最值问题等常见题型的解题方法. 关键词：二次函数；综合性题目；解题方法二次函数是初中数学知识体系的重要构成，依托
解题天地 | 构造图形，以形解数

解题天地 | 构造图形，以形解数

摘要：构造图形解决代数问题的依据和思路是数形结合思想，通过由“数”到“形”的巧妙转换，将原本繁琐的代数问题转化为简洁的几何问题来解决，具有“化繁为简，直观易懂，便于解答”的特点.构造几何图形的关键是善于通过对实际问题的分析，抓住其本质，联想到相应的几何图形，建立数学表达式，并应用其性质找到解决问题的途径.本文中通过对典型例题的解析、方法对比与“一题多解”式的拓展演练，从一个侧面展示了运用构造法解题
解题天地 | 反比例函数图象中的一个基本图形的应用

解题天地 | 反比例函数图象中的一个基本图形的应用

1 基本图形与结论展示如图1，反比例函数y＝kx的图象上有两点A，B，过A，B分别作x轴的垂线，垂足分别为C，D，那么S△AOB＝S梯形ACDB. 证明：四边形OABD的面积S＝S△AOC＋S梯形ACDB. 从另一角度，四边形OABD的面积S＝S△AOB＋S△BOD，而S△AOC＝S△BOD，所以S△AOB＝S梯形ACDB. 2 运用结论，简洁明快 2.1 与矩形结合，求点的坐标再运用
解题天地 | 初中数学二次函数解题方法与技巧

解题天地 | 初中数学二次函数解题方法与技巧

基于中考数学试题的研究可以发现，二次函数的知识点在初中数学试卷中所占比例较大，内容较多，题目较复杂，考题难度较大.特别是二次函数问题经常会在中考压轴题中出现.下面对有关二次函数的常见题型及解题方法进行总结. 1 解析式问题——找、代、解在求解二次函数解析式的问题中，教师可以引导学生遵循“找、代、解”的解题思路，解决与二次函数有关的实际问题. 例1 如图1所示，对称轴为直线x=12的抛物线
解题天地 | 圆中不规则图形面积解法探析

解题天地 | 圆中不规则图形面积解法探析

在几何中，面积是一个重要的概念，用于量化平面图形所占据的空间大小.对于规则图形，我们可以简单地使用相应的公式计算出其面积，例如长方形的面积等于长度乘宽度，三角形的面积等于底边乘高除以2.然而，当面对不规则图形时，这些简单的公式就无法直接适用.不规则图形指没有明确规则形状的图形，如弯曲的边界线、多边形的组合等.这些图形的面积无法通过简单的公式计算得出，面积的计算变得更为复杂和困难，需要采用特定的方法
解题天地 | 善析条件结论，实现一题多解

解题天地 | 善析条件结论，实现一题多解

摘要：几何证明在中学数学教学中有着重要的作用，同时也是考卷中的重点考查部分.学生面对几何证明题一筹莫展的重要原因之一是缺乏分析能力，不善于运用数学思维分析题目条件和结论，从而失去提升数学解题能力的机会.在教学中，教师应引导学生用所学知识分析思考，实现知识间的融会贯通，同时引导学生在不同视角下对题目进行多角度分析思考，实现一题多解. 关键词：初中几何；解题技巧；一题多解 1 问题呈现如图1，
教师发展 | 新课标背景下构建“学为中心”数学复习课堂的策略

教师发展 | 新课标背景下构建“学为中心”数学复习课堂的策略

摘要：“教”是为了“学”，构建“学为中心”的初中数学复习课堂就是从学生的“学”出发设计教学，发展学生的数学素养.以“一次函数的图象和性质”的复习课教学为例，通过巧妙创设情境引发学生兴趣和欲望，借助合作学习和捆绑评价实现学生能力的发展与提高，发展数学核心素养. 关键词：学为中心；复习课；一次函数的图象在课堂教学中落实学生的主体地位，即构建以“学”为中心的课堂教学，强调学生的学习主动性，尊重学生
教师发展 | “追”出兴趣，“问”来思维

教师发展 | “追”出兴趣，“问”来思维

摘要：灵活且有深度的追问可以诱发学生的探究兴趣，使其在自主思考和深度探究中向着知识深处漫溯.本文中借助多个具体实例，简要论述课堂追问的时机，引领学生走数学研究之路，发展学生的数学核心素养. 关键词：追问；数学思维；核心素养 “行是知之路，学非问不明.”课堂教学不仅需重视设问，还需要关注追问，且都需要问得巧、问得妙，才能亦启亦导，拨动思维之弦，激发探究热情，从而在自主探究和合作学习中生成智慧，获
教师发展 | 正视课堂生成打造精彩课堂

教师发展 | 正视课堂生成打造精彩课堂

摘要：在数学课堂教学中，教师会精心准备、充分预设，以确保教学目标的顺利达成.但是若教学中过度依赖预设，可能也会错失许多精彩的生成.因此，在数学课堂教学中，教师应预留时间和空间让学生独立思考，自主探索，并及时捕捉各种有效的课堂生成，通过合理的开发与利用来提高教学有效性，提升教学品质和教师素养. 关键词：预设；生成；有效性课堂是丰富多彩的、动态变化的.在数学教学中，教师会认真研究，精心筹备，充分
教师发展 | 着眼素养培育的问题化学习

教师发展 | 着眼素养培育的问题化学习

摘要：问题化学习指以学生学习为主线，以问题为载体，以自主学习、合作学习、体验探究学习为方式，以获得真实的学习体验为特征，以发展问题意识为导向，以培养数学素养为目标的教学方法.本文中首先揭示数学素养培育与问题化学习的内在关联，并以初中数学复习课教学为例探寻问题化学习的实践策略，为一线教师提供实践参考. 关键词：问题化学习；数学素养；二次函数学生良好的数学素养培育无法在师讲生听的学习模式中获得，
教师发展 | 项目式学习驱动下初中数学实践活动的路径探究

教师发展 | 项目式学习驱动下初中数学实践活动的路径探究

摘要：新课标的颁布，为当前数学教学改革提供了新的思路和方向.新课标强调教师应当从整合、统一的视角出发，将数学学习、思维探究与问题解决的全程概括于优质的项目之下，使学生在以项目任务为总体框架的实践活动中获得进步.本文中从“项目式学习”的视角出发，探索其与数学实践活动的内在关系，着重阐述项目式学习驱动下完整的数学实践活动的教学流程，并总结了其开展策略. 关键词：项目式学习；数学实践活动；路径探究
教师发展 | 初中数学项目式教学设计

教师发展 | 初中数学项目式教学设计

摘要：在“双减”和新课标的背景下，以解决真实复杂问题为导向的教学方法——项目式教学，成为各学校教师努力的方向，项目式教学也更注重培养学生的核心素养，鼓励学生将知识应用到生活中去解决实际问题.本文中将以北师大版初中数学九年级上册综合与实践部分的“制作视力表”为内容，展开项目式教学设计. 关键词：项目式教学；初中数学；图形的相似近年来，“双减”和新课标中都重点提出了核心素养的概念，相对于传统观念
教师发展 | 初中数学概念课教学设计

教师发展 | 初中数学概念课教学设计

摘要：数学概念是抽象化的，对新概念的认知需要具有一定的抽象思维能力.要正确地认知和构建一个数学概念，必须明确这个数学概念的内涵及外延，也就是明确概念的“质”的特征和“量”的范围.初中生的思维结构虽日趋稳定，但并未完整与系统化，仍然以形象思维为主导.虽然学生在学习“反比例函数”之前，已经对一次函数的概念、图象和性质以及应用有所掌握，但面对反比例函数时，或多或少存在模糊不清的感觉，这就需要教师在课堂教
教师发展 | 立足生本理念聚焦问题设计促发深度学习

教师发展 | 立足生本理念聚焦问题设计促发深度学习

摘要：立足生本理念，以具体问题为载体，以自主合作探究为途径，可以自然促发深度学习，无痕发展学生的数学思维和数学素养.本文研究者结合“反比例函数”的教学设计，理性探讨生本理念下深度学习的问题设计策略，从真正意义上让学生学会思维，提高数学核心素养. 关键词：生本理念；问题；深度学习 1 提出问题教师是学生学习活动的“引起、维持和促进者”.在学习过程中，学生作为学习的主体，在教师的指导、启发和点
教师发展 | 巧设问题促理解放慢节奏促提升

教师发展 | 巧设问题促理解放慢节奏促提升

摘要：学习是一个不断发展、不断积累的过程.教学中，教师应从学生已有知识和生活经验出发，为学生预留充足的时间和空间去思考、去交流、去探索，让学生经历知识的形成、发展、应用等过程，提升学生的数学能力，落实学生的核心素养. 关键词：过程；数学能力；核心素养在传统数学教学中，部分教师为了片面地追求速度，常以强灌的方式将知识呈现给学生，然后通过“题海战术”来提升学生的解题技能.从短期来看，“讲授+练习
教师发展 | 指向深度学习的初中数学课堂教学策略探究

教师发展 | 指向深度学习的初中数学课堂教学策略探究

摘要：深度学习立足于真实情境的问题解决，注重学生高阶思维的发展，为初中常态课教学设计打开了创造之窗，开辟了探索之径.基于对深度学习的认识，通过“相似三角形的判定”的部分教学片段，进而去理性探讨深度学习的初中数学课堂教学策略. 关键词：深度学习；课堂教学；相似三角形 1 提出问题所谓“深度”，就是触及事物内部与事物本质的程度.深度学习是在记忆和理解的基础之上，在主动分析、应用之后，可以创造与

过往期刊

更多

猜你喜欢

苏州工业园区教育局电子阅览室