全部分类/
中学教育/
中学数学·高中版

中学数学·高中版

2024年11期

扫码免费借阅

目录

快速导航

特色展台 | 2023年新高考全国Ⅱ卷第22题探究

特色展台 | 2023年新高考全国Ⅱ卷第22题探究

题目（1）证明：当0<x<1时，x－x2<sin x<x；（2）已知函数f（x）=cos ax－ln（1－x2），若x=0是f（x）的极大值点，求a的取值范围. 1 试题目标命题考查点：利用导数证明不等式，已知极值点求参数范围，与三角函数相关的导数. 思想方法：函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想. 能力要求：抽象概括、推理论证.
特色展台 | 多角度拓思维研一题通一类

特色展台 | 多角度拓思维研一题通一类

摘要：本文中针对2023年全国甲卷理科第16题，在研究其若干解法的基础上，溯源人教A版新教材，总结求解“爪型”三角形的通法，探究问题的本质以及变式题的编制. 关键词：“爪型”三角形;一题多解;全国甲卷理科第16题 1 真题呈现（2023年全国甲卷理科第16题）在△ABC中，AB=2，∠BAC=60°，BC=6，D为BC上一点，AD为∠BAC的平分线，则AD=. 2 解法探究数学家波利
课程视点 | 数学史融入高中数学课堂的实践探讨

课程视点 | 数学史融入高中数学课堂的实践探讨

《普通高中数学课程标准（2017年版2020年修订）》指出，数学文化应融入高中数学教学活动，教师应有意识地引导学生了解数学的发展历程，感悟数学的价值，提升学生的学科精神、应用意识和人文素养，激发学生的数学学习兴趣，开拓学生视野，提升数学学科核心素养.数学史是一种非常重要的教学资源，是渗透数学文化的有效途径之一.教师通过还原数学历史或结合学生的认知水平适当地改编历史，将数学史融入数学教学活动中，有助
课程视点 | 新人教版高中数学教材中一道三角函数应用题的商榷

课程视点 | 新人教版高中数学教材中一道三角函数应用题的商榷

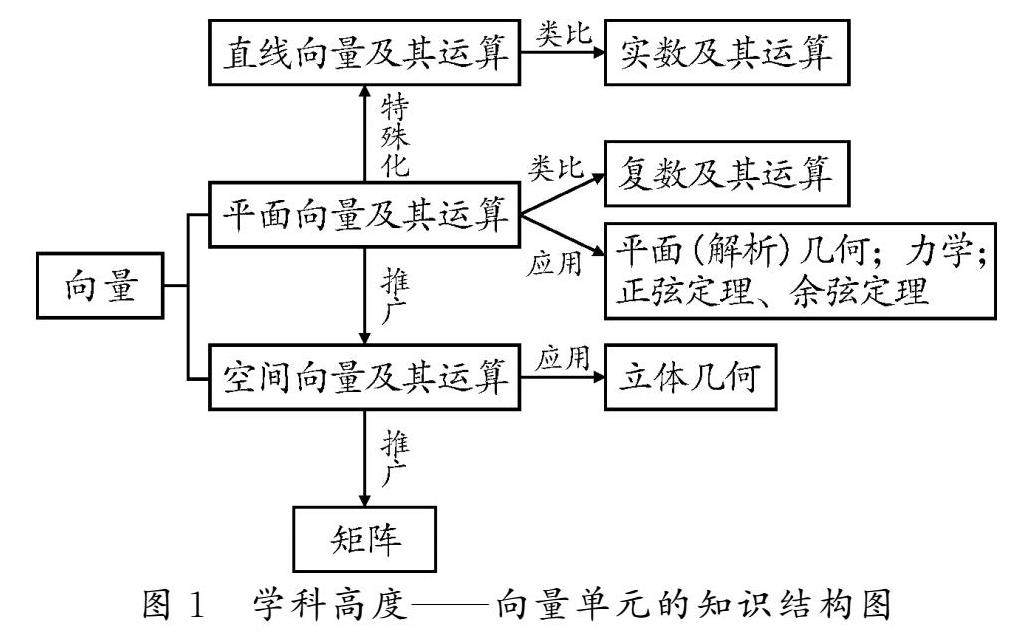
摘要：针对2019年新出版的人教A版普通高中教科书·数学必修第一册第五章“三角函数”的第7节“三角函数的应用”的例2做了深入探讨，提出了不同的见解. 关键词：三角函数；吃水深度；新教材 1 教材中的例题在2019年新出版的人教A版普通高中教科书·数学必修第一册（下称“新教材”）中，笔者发现第五章“三角函数”的第7节“三角函数的应用”的例2值得探讨，原题呈现如下：例2 海水受日月的引力，
教法探索 | 基于核心素养的高三数学复习课单元教学设计策略

教法探索 | 基于核心素养的高三数学复习课单元教学设计策略

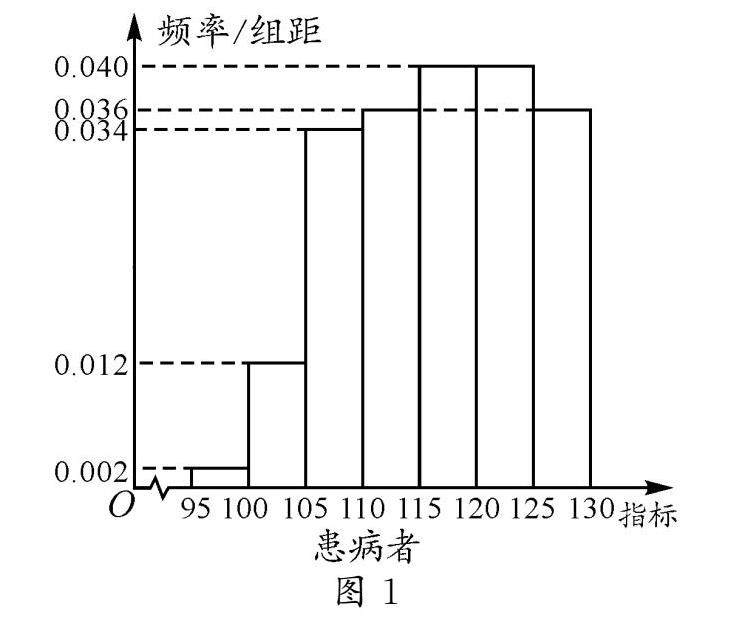
摘要：高三作为高中数学学习的特殊阶段，为学生核心素养、思维能力的培养提供了难得的机会.怎样在高三数学复习课中改变相对固化的试题形式、减少死记硬背和机械刷题，以适应高考改革中重视学科知识本质与通性通法的要求呢？本文认为应居高临下，采用单元教学，从整体上把握教学内容，优化整合知识点.由此提出了基于核心素养的高三数学复习课单元教学设计的四条策略，即站在学科高度、聚焦核心知识、思考知识本质、感悟解题思想，
教法探索 | 透视高考真题关注数学阅读

教法探索 | 透视高考真题关注数学阅读

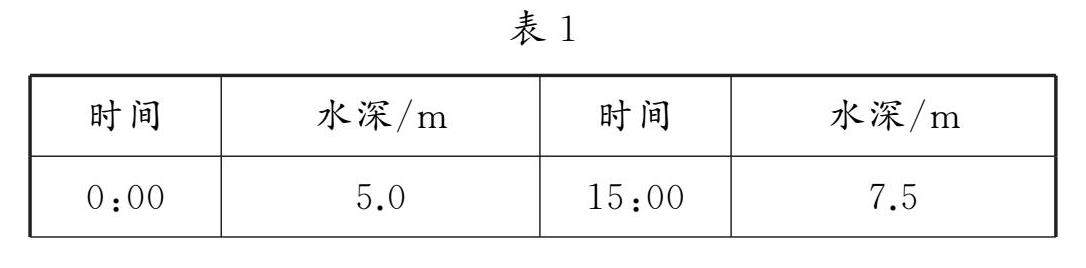
摘要：结合近几年全国卷高考真题，在反套路、反刷题上下功夫，注重创新类试题创设真实情境，同时新教材增加了许多数学阅读内容，对数学阅读提出了很高的要求，因此在教学中要引导学生关注数学阅读，提升学生阅读能力. 关键词：高考真题；关注；数学阅读；能力考查 1 数学阅读及数学阅读能力 1.1 数学阅读的定义 “数学阅读”不同于一般的阅读，数学阅读是从数学阅读文本中获取有用信息进行内化、理解、推理与反
教法探索 | 高中数学建模素养培养案例分析

教法探索 | 高中数学建模素养培养案例分析

摘要：通过建模将实际问题转化为数学问题，进而利用数学知识解决问题，用模型解释现实生活中与数学知识有关的现象与规律.本文中以“三角函数的应用”为例，详细分析了数学建模的过程，旨在促进学生数学建模素养的培养. 关键词：新课标；高中数学；建模素养；培养案例新课标背景下高中数学建模素养的培养越来越受到重视.本文中以“三角函数模型简单应用”的一个实际教学案例为例，展示如何引导学生在分析问题、解决问题的
教法探索 | 动态与静态的巧妙融合：一道抛物线题的破解

教法探索 | 动态与静态的巧妙融合：一道抛物线题的破解

摘要：依托一道高考模拟题中的抛物线问题，借助问题的动态与静态的巧妙融合，从代数、距离、焦半径等不同思维视角切入，开拓数学思维，拓展解题技巧，合理变式拓展，进行深度学习与探究学习，引领并指导数学教学与解题研究. 关键词：抛物线;动点;代数;距离;焦半径直线与抛物线的位置关系的综合问题，是高考命题的一类基本类型.此类问题，基于抛物线自身所具有平面解析几何的基本属性，或者曲线所对应的平面几何的
教法探索 | 教学聚焦，“图”谋天下

教法探索 | 教学聚焦，“图”谋天下

摘要：在资源有限的情况下，我们应该聚焦整合资源，找准方向，作用于一个点.方向就是设计数学基本活动，引领学生理解数学本质.教学可以围绕“图”展开，只要抓住了作用点“图形”，帮助学生实现数学课程目标，学生定能“图”谋天下. 关键词：聚焦；图形；备考；教学 1 聚焦整合资源，找准方向高考改革已进入深水区，对于高中教师只有认真研读“新课程、新教材、新高考”，才能引领学生“图”谋天下，取得更好的成绩
教法探索 | 情境创设，概念教学

教法探索 | 情境创设，概念教学

摘要：概念教学是高中数学教学中一个非常重要的环节，也是充分展示教师能力水平与教学经验的场所，设计契合教学规律，落实核心素养，适合学生思维习惯，引起学生共振的教学设计是教师不断追求的目标.结合三角函数的概念教学，合理创设情境，巧妙设置问题，优化教学过程，完善教学设计，做了一个很好的尝试. 关键词：三角函数；概念；正弦；余弦；正切；教学设计 1 教材分析三角函数是在学习了函数的基本概念，以及幂
教法探索 | 一节探究抛物线性质“y1y2=-p2”的专题讨论课

教法探索 | 一节探究抛物线性质“y1y2=-p2”的专题讨论课

专题讨论课是师生在学习过程中以某个教学内容为中心，在教师的指导下，学生先自学，再进行课堂讨论的教学模式.高中数学在某些章节内容上完后，可以适当地开展专题讨论课.通过这种方式，既可以加深对所学内容的理解，又可以促使学生产生新的想法，开阔眼界和思路，培养他们独立思考的能力. 1 专题讨论课的步骤专题讨论课的开展一般包含以下四步：（1）教师事先根据学生遇到的问题或难点，和学生共同商定研究主题，
学生学习 | 圆锥曲线综合探究类题型赏析

学生学习 | 圆锥曲线综合探究类题型赏析

摘要：探究性问题是近年来高考数学中出现的新题型，其中圆锥曲线综合探究类试题包括探究条件、探究结论、创新探究、综合探究等类型，不仅涉及到的知识点多，而且对观察、猜测、分析、类比、转化、计算、证明等能力也有较高的要求，属于分值高、难度大的题型.解决这类问题，要打破常规，灵活运用“数形结合”“大胆假设，小心求证”“从一般到特殊，从特殊到一般”“转化变形”等数学思想与方法. 关键词：是否存在问题；对称问
学生学习 | 三角形面积公式的向量形式及其应用

学生学习 | 三角形面积公式的向量形式及其应用

要结论.本文中结合三角形面积公式的向量形式对应定理的给出，进行合理推广与拓展，借助实例加以剖析与应用，抛砖引玉. 1 三角形面积公式的向量形式的定理和推论引入平面向量的相关知识后，可以用平面向量及其相关知识来处理三角形面积公式，得到三个与平面向量形式有关的三角形面积公式的结论. 1.1 向量面积公式定理在△ABC中，若AB=a，AC=b，则△ABC的面积为S=12（|a|＼5|b|）
学生学习 | “局部缩小”在不等式恒成立问题中的应用

学生学习 | “局部缩小”在不等式恒成立问题中的应用

利用导数处理不等式恒成立问题中的参数范围求解时，对于参数如何分类讨论，学生普遍感到“入口宽、下手难、分不全”.为此，我们可以在分类讨论的基础上，利用不等式恒成立的定义或者端点取值局部缩小参数的取值范围，帮助学生解决困惑，提高此类问题的正确率. 局部缩小的方法实际上是一种必要性探究法，针对某些函数恒成立问题，通过恒成立的定义或者端点取值的方法，得到不等式成立的一个必要条件，进而缩小参数的范围，降低
学生学习 | 例谈充分性在解题中的应用

学生学习 | 例谈充分性在解题中的应用

摘要：在进行解题教学时要善于思考，弄清楚知识的来龙去脉，这样才能让学生透过现象看到本质，从而达到“一览众山小”的教学境界，唯如此方是我们的教学之道. 关键词：充分性；应用；现象；本质匈牙利著名数学家G＼5波利亚有一句名言：掌握数学就意味着解题.在平时的数学学习中，学生和老师每日都离不开解题，但如何解答数学问题成为当下师生关心的共同话题.每次考完试，总会听到学生感叹：这个题目我就差一步——检验
学生学习 | 全概率与贝叶斯公式解题策略探究

学生学习 | 全概率与贝叶斯公式解题策略探究

1 全概率公式全概率公式主要是解决对某一个过程中已知条件求出最后结果的概率方法，在学习的过程中，可以结合古典概型来理解和运用全概率公式求解概率问题.该公式主要解决的问题：当某个事件的概率直接计算比较费劲的时候，可以用与该事件有联系的n个两两互斥的事件将该事件进行分割，然后根据加法公式和乘法公式求出该事件的概率，这种解决问题的思想可以将事件化难为易，利用简单事件的运算表示复杂事件，再根据概率公式
学生学习 | 揭示知识本质提升核心素养

学生学习 | 揭示知识本质提升核心素养

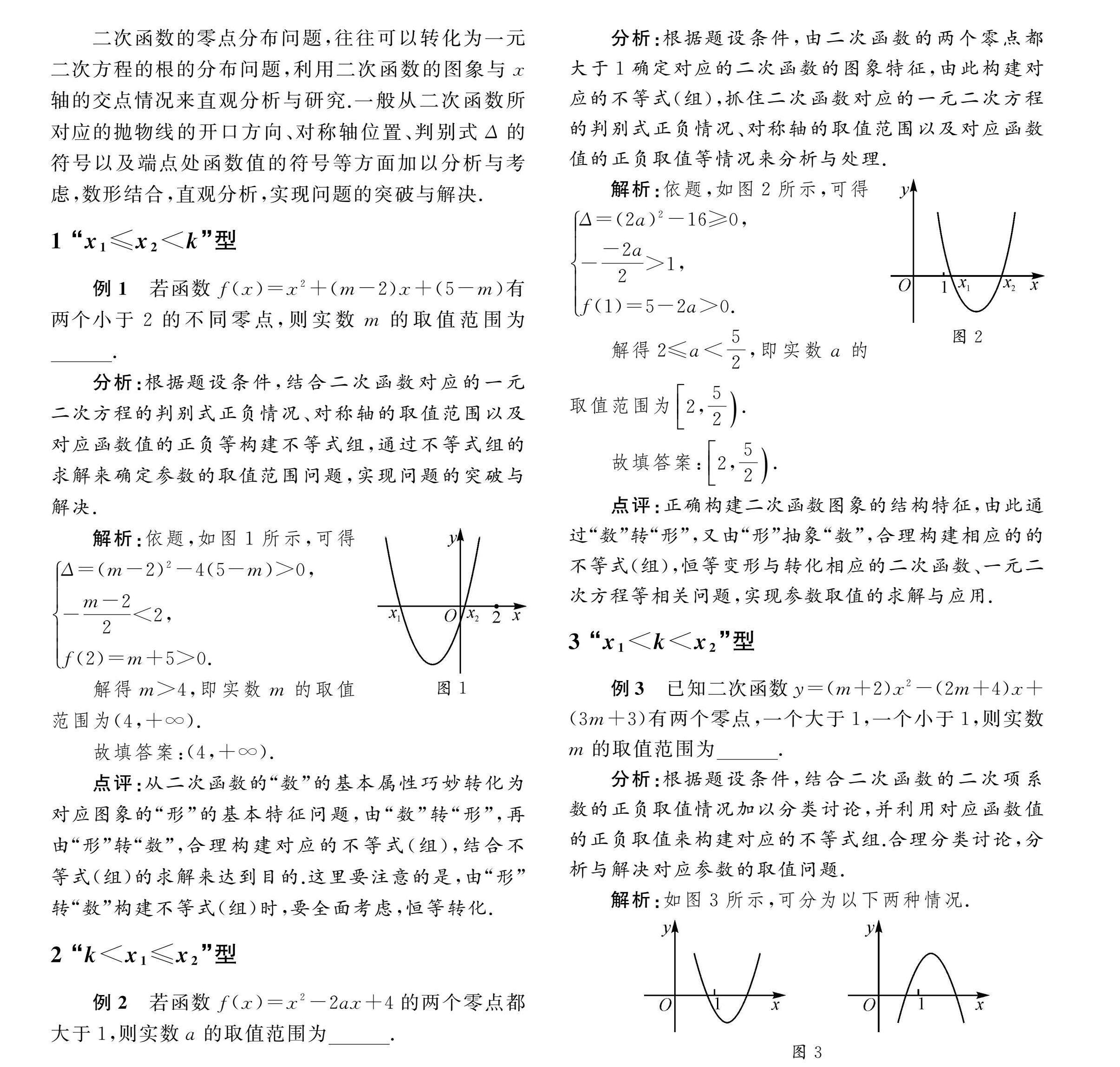
解三角形问题中的“爪”型结构，成为了最近几年高考命题的新宠.所谓“爪”型结构，即在给定的三角形内，通过连接某一顶点与对边上任意一点，构建出一种形似爪子的几何形态，该问题往往聚焦于三角形的三大核心元素——中线、高线及角平分线来检验学生的数学综合能力.这类问题不仅要求学生具备扎实的数学运算功底，还需具备逻辑思维能力、转化与化归思想，以及函数与方程思想等数学素养. 1 解三角形中有关中线问题在解决
学生学习 | 二次函数的图象性质与零点分布

学生学习 | 二次函数的图象性质与零点分布

摘要：涉及二次函数的图象性质与对应的零点分布问题，是二次函数、二次方程与二次不等式问题中最为常见的一类基本问题.结合二次函数的图象性质与零点分布情况，通过不同类型就对应实例的剖析，挖掘问题的内涵与实质，归纳解题技巧与策略，有效指导数学教学与学习. 关键词：二次函数；方程；不等式；图象；性质二次函数的零点分布问题，往往可以转化为一元二次方程的根的分布问题，利用二次函数的图象与x轴的交点情况来直
学生学习 | 巧借特殊思维，妙破解析几何

学生学习 | 巧借特殊思维，妙破解析几何

一般思维与特殊思维是辩证思维模式中的两种方式，二者之间又是辩证统一的.在解决一些客观题时，特别是有确定答案的选择题或填空题时，借助场景应用，合理选用特殊思维，使得一般性问题特殊化，从中寻找分析与研究问题的一般性规律，给问题的突破与求解开拓一个全新的局面. 在处理平面解析几何问题时，借助直线、圆、圆锥曲线等相关曲线的内涵与实质，优化其“数”的基本属性与“形”的结构特征，以特殊思维巧妙切入，借助特殊
学生学习 | 数学解题教学中解题过程严谨性及规范性探究

学生学习 | 数学解题教学中解题过程严谨性及规范性探究

摘要：在高中数学解题的过程中，不仅要确保解题过程正确、清晰、简洁、完整，同时还必须要保证其规范性.规范性的解题，有助于学生建立起解题的思维框架，避免思维混乱和跳跃，能帮助学生培养逻辑思维和推理能力，提高解题的准确性.本文中以不等式证明为例，深入研究解题过程规范性的要求，结合实例分析给出了培养解题过程规范性的方法和技巧，最后对解题教学提出了一些启示和建议. 关键词：高中数学；规范性；不等式证明
评价透视 | 2024年高考题中的高阶思维能力考查

评价透视 | 2024年高考题中的高阶思维能力考查

在新教材（人民教育出版社2019年国家教材委员会专家委员会审核通过）、新课程（《普通高中数学课程标准（2017年版2020年修订》）、新高考的“三新”背景下，高中数学教学与学习必须更多地去关注数学基础知识的发生、经历与发展过程，注重学生数学思维能力的发展，特别是高阶思维能力，从而促进学生的深度学习，为学生的终生学习创造条件、奠定基础.本文中结合2024年高考数学真题的剖析，从高考命题与考查方向等层
评价透视 | 特殊思维巧应用，高考真题妙解答

评价透视 | 特殊思维巧应用，高考真题妙解答

摘要：特殊思维与方法是解决数学问题“通性通法”的升华与提升，成为快速简捷处理数学客观题的一种最为有效且灵活的基本思维方式.结合2024年高考真题中的几个实例，借助特殊思维与方法的巧妙应用，从不同知识点与应用场面加以展开，优化过程提升效益，总结特殊思维与方法的解题技巧与规律，指导高考数学的复习备考与优化解题. 关键词：高考数学；特殊思维；函数；数列特殊思维与方法，是解决数学问题中最具特色的一种
评价透视 | 抓住本质，从一般到特殊命制试题

评价透视 | 抓住本质，从一般到特殊命制试题

摘要：圆锥曲线中有许多二级结论，这些结论是教材知识的进一步延伸，利用它们能快速解答问题，也可以利用它们引入特殊化思想命制试题.本文中以教材推导椭圆标准方程的过程为背景，分析推导过程中一些式子的几何意义，得出结论，利用此结论命制了一个定值、定点问题. 关键词：椭圆；斜率；定点；定值 1 试题呈现原题（人教A版选择性必修第一册第108页）设A，B两点的坐标分别为（－5，0），（5，0）.直线
评价透视 | 一道高中数学典型例题的素养分析及命题启示

评价透视 | 一道高中数学典型例题的素养分析及命题启示

《普通高中数学课程标准（2017年版2020年修订）》强调：数学运算素养是学生解决数学问题的基础，逻辑推理素养是学生分析问题和得出结论的关键，直观想象素养则帮助学生将抽象的数学概念具体化.这三种素养相互依托，共同构成学生全面解决问题的能力，是数学教育中的重要目标和考查重点. 1 典型例题及解析题目（多选题）已知正方体ABCD-A1B1C1D1的棱长为2，O是空间中的一动点，下列结论正确的是
解题天地 | 一道高考解析几何压轴题的探究

解题天地 | 一道高考解析几何压轴题的探究

1 题目呈现（2020全国卷）已知A，B分别为椭圆E：x2a2+y2=1（a>1）的左、右顶点，G为E的上顶点，AG·GB=8，P为直线l：x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D. （1）求E的方程；（2）证明：直线CD过定点. 2 题目剖析第（1）问直接运用题目条件可求出E的方程：由椭圆方程E：x2a2+y2=1（a>1），可得A（－a，0
解题天地 | 2023年新高考Ⅰ卷第17题的多解、溯源、变式

解题天地 | 2023年新高考Ⅰ卷第17题的多解、溯源、变式

高考真题是命题专家集体智慧的结晶，既具有选拔功能，又对教学起着导向作用.教师只有深入研究高考真题，才能提高教学效益.下面是笔者对2023年新高考Ⅰ卷第17题的一些思考，与大家交流. 1 考题再现（2023年全国高考数学新高考Ⅰ卷第17题）已知在△ABC中，已知A+B=3C，2sin（A－C）=sin B. （1）求sin A; （2）设AB=5，求AB边上的高. 这是一道解三角形与三角
解题天地 | 岁岁年年“题”不同，年年岁岁“解”相似

解题天地 | 岁岁年年“题”不同，年年岁岁“解”相似

不等式恒成立求参数问题既是高考热点问题，也是重点问题．纵观近年来高考试题都有考查，试题强调对知识的综合运用和能力的综合考查，有效地考查了学生对函数、不等式、导数知识的掌握情况，同时也考查了学生的转化与化归、数形结合、分类讨论、极限等数学思想．试题具有创新性，重视体现思维过程，并且计算合理，有利于选拔创新性人才．下面以2023年与2024年新高考具有代表性的压轴题为例，探究求解策略，深入研究与思考，
解题天地 | 三角搭台导数唱戏：探究与三角函数交汇的函数导数问题

解题天地 | 三角搭台导数唱戏：探究与三角函数交汇的函数导数问题

摘要：以三角函数为载体的函数导数问题，在近年高考试题中频频出现.文章以几道2023年高考试题为例，探究该类问题的一般求解策略. 关键词：三角；导数；求解策略 2023年高考新高考全国卷Ⅱ第22题，全国甲卷理第21题、文第20题均考查以三角函数为载体的导数问题.该类问题由于对三角函数无论进行几次求导，仍含有三角函数，成为解题中的难点.下面笔者以2023年高考试题为引例，探究该类问题解题策略，以期
解题天地 | 重心巧创新，向量妙“包装”

解题天地 | 重心巧创新，向量妙“包装”

摘要：三角形的重心作为平面几何中的一个基本知识点，具有良好的几何性质与创设场景，往往在解三角形、平面向量、解析几何等相关问题中具有非常重要的价值.结合一道抛物线模拟题，就三角形重心背景下的解析几何问题加以剖析，多思维视角切入，多技巧方法破解，总结解题技巧规律，启示教学应用与解题研究. 关键词：抛物线；向量；重心；坐标；面积三角形中的“心”（重心、内心、外心、垂心、旁心）问题，是初中平面几何的
解题天地 | 挖掘问题本质，实现“一题多解”

解题天地 | 挖掘问题本质，实现“一题多解”

三角最值问题一直是高考数学试卷中的常见热点题型之一，可以合理并巧妙融合三角函数的基本概念与基本公式、函数与方程、不等式等相关知识，实现不同知识模块间的交汇，这也为此类三角最值问题的解决提供了方式各异的数学思维视角与切入点，是充分展示知识交汇、体现方法多样性的一大重要场所. 1 问题呈现问题（2023年北京大学优秀中学生寒假学堂数学测试）设x，y∈0，π2，则1cos2x+1sin2xsin
解题天地 | 特殊值法巧用，高考真题妙解

解题天地 | 特殊值法巧用，高考真题妙解

特殊值法思维是解决数学问题中最为特殊的一种“巧技妙法”，是解决问题的“通性通法”的升华与提升.特别，在历年高考数学试卷的一些客观题的解答中，借助特殊值（不同场景，对特殊值有不同的类型变化）的选取，巧妙利用特殊值法，可以非常简捷地处理一些相关问题，真正达到“小题小做”“小题巧做”“小题快做”等良好解题效益，倍受师生喜欢与追求.本文中结合2023年高考数学真题，就一些客观题中特殊值法的合理选用与巧妙应
解题天地 | 棱台场景创设，线面角求解

解题天地 | 棱台场景创设，线面角求解

摘要：立体几何中的空间角是历年高考试卷中的常客之一，备受高考命题者所垂青，成为新高考数学试卷中的一个基本考点.结合一道高考真题，以棱台场景创设，通过立体几何中的线面角的设置与求解，从不同数学思维角度切入，结合不同的数学方法来破解，总结规律，有效指导数学学习与教学. 关键词：正三棱台；体积；线面角；正切立体几何中的空间角（异面直线所成的角、线面角、二面角等），可以比较集中且有效地考查学生的空间
解题天地 | 含参函数奇偶性，方法与素养齐飞

解题天地 | 含参函数奇偶性，方法与素养齐飞

摘要：函数奇偶性作为函数的基本性质之一，是历年高考数学中的一大基本考点，经常以小题（选择题或填空题）形式出现，难度适中，变化多端.结合2023年高考数学新高考Ⅱ卷第4题，以含参的复杂函数的奇偶性来确定参数值，归纳剖析解题技巧与方法，链接高考，变式拓展，指导数学教学与复习备考. 关键词：函数；奇偶性；参数；定义；性质函数奇偶性是历年高考数学中对函数模块知识的重点考查内容之一，常考常新，变化多端
解题天地 | 存在性判定，思维性应用

解题天地 | 存在性判定，思维性应用

摘要：圆锥曲线中的存在探究性问题是一类全面考查数学知识与数学能力的综合应用问题，通常是高考中的一大热点与难点.结合一道椭圆解答题中存在性探究实例，以创新场景创设，就点的存在性问题加以合理判定与思维性应用，归纳解题技巧方法与策略规律，指导解题研究与复习备考. 关键词：椭圆；动点；切线；等差数列；存在探究性问题通常是高考中备受命题者青睐的一种题型.而圆锥曲线中的探究性问题，更是该模块命题的常见题
解题天地 | 问题深入挖掘，思维合理发散

解题天地 | 问题深入挖掘，思维合理发散

摘要：涉及分段函数的综合应用问题是历年高考中的常考题型之一，难度中等，背景多变，形式多样，是数学基础知识与基本技能交汇与融合的一大重要载体.结合一道高考真题，借助分段函数的场景创设与函数单调性的应用，合理剖析方法技巧，总结规律策略，有效指导数学教学与解题研究. 关键词：分段函数；单调性；直接；排除；导数涉及分段函数的综合应用问题，是历年高考中的热点与难点问题之一，也是高考试题中的一类常见题型
解题天地 | 拓展数学思维，总结解题技巧

解题天地 | 拓展数学思维，总结解题技巧

涉及函数值、参数值或代数式等的大小比较问题，是近年新高考数学中一类创新热点与基本考点.此类问题以各种创新新颖的方式加以设置，常考常新，形式多样，变化多端，而万变不离其宗，问题中都巧妙融合了幂函数、指数函数或对数函数，以及三角函数等基本初等函数模型，通过对应函数的图象与基本性质，以及不等式的基本性质等相关内容来交汇与融合，充分落实并贯彻新课标中“在知识交汇点处命题”的命题思想.同时此类问题，有时还创
解题天地 | 把握三次函数本质，巧思妙解综合应用

解题天地 | 把握三次函数本质，巧思妙解综合应用

摘要：三次函数及其综合问题作为典型函数模型，在近年的高考、竞赛试题中频繁出现，成为“出镜率”很高的函数模型之一.通过对一道三次函数高考真题的展示，结合多思维视角切入，妙层次分析挖掘，总结归纳结论，全面提升解题能力. 关键词：三次函数；零点；极值；对称轴；对称中心在新课标高考数学试卷中，以三次函数为情境的函数与导数的综合应用问题，是知识综合与技能应用中的一类基本考点.借助三次函数的应用场景，结
解题天地 | 巧思维展开，妙方法应用:一道椭圆解答题的探究

解题天地 | 巧思维展开，妙方法应用:一道椭圆解答题的探究

涉及直线与圆锥曲线的综合应用的解答题，常常巧妙融入“动态”与“静态”的变化过程，交汇“动点”与“定点”的变形转化、“常值”与“最值”的合理过渡，同时有“数”的本质属性，又有“形”的几何特征，新颖多变，具有较高的区分度与较好的选拔性，是全面考查学生的“四基”与数学基本能力，以及培养数学核心素养的一个重要题型. 1 问题呈现问题在平面直角坐标系xOy中，点F（－3，0），P（x，y）是平面内的
解题天地 | 2024年高考数学新高考Ⅱ卷第15题的探究

解题天地 | 2024年高考数学新高考Ⅱ卷第15题的探究

解三角形的基本应用问题，是综合解三角形与三角函数这些主干知识的一个基本考查点，也是高考数学的一个重要考查点.此类问题，往往依托初中平面几何图形的应用场景，联系起高中的解三角形、三角函数等相关知识，合理构建初、高中阶段知识的联系与应用，同时也交汇高中数学中的函数与方程、平面向量等其他相关知识，充分落实新课标中“在知识交汇点处命题”的高考基本指导思想，备受各方关注. 1 真题呈现高考真题记△A
解题天地 | 深挖命题内涵，多解变式应用

解题天地 | 深挖命题内涵，多解变式应用

摘要：数学解题不能只停留在问题解答上，合理挖掘命题的本质内涵，巧妙进行“一题多解”“一题多变”等，给解题拓展更加宽广的空间.本文中借助一道高考真题，结合两个含参的函数所对应曲线的交点个数情况，合理挖掘内涵，巧妙创新应用，归纳总结规律与性质，指导数学教学与复习备考. 关键词：函数；曲线；交点；偶函数；数形结合分析与解决数学问题的本质，就是合理探究问题的内涵与实质，化“生”为“熟”，巧妙变换，可
解题天地 | 巧思维开拓思路，妙应用变式拓展

解题天地 | 巧思维开拓思路，妙应用变式拓展

作为平面向量模块中最重要的基本知识之一，平面向量的数量积及其综合应用问题成为近年高考试卷中的一个基本考点.特别是涉及平面向量数量积的求值与应用问题，以各种形式的场景创设，借助数量积的形式来变形与转化，基于平面几何，依托平面向量，融合函数与方程、三角函数、基本不等式等其他相关知识，成为该模块知识中考查的重中之重，也是课堂教学与复习备考中的一个基本专题，成为全面考查数学“四基”与“四能”的一个重要场所
解题天地 | “数”“形”思维切入，位置关系突破

解题天地 | “数”“形”思维切入，位置关系突破

摘要：基于直线与圆锥曲线的位置关系，特别是有关相交或相切的问题，是高考命题的一个常见考点.结合一道直线与双曲线相交的高考试题，从“数”与“形”的视角来切入，合理剖析与应用，归纳总结解题技巧与策略方式，指导数学教学与解题研究. 关键词：直线；双曲线；相交；斜率；方程在圆锥曲线的综合应用问题中，有关直线与圆锥曲线之间的位置关系以及与之相关的综合应用问题，成为历年高考命题中的一个基本考点.基于直线
解题天地 | 2023年高考数学全国甲卷理科题11的探究

解题天地 | 2023年高考数学全国甲卷理科题11的探究

摘要：立体几何综合应用问题的解题思维视角往往多变，切入点众多，是全面考查基础知识与基本能力等方面的一个重要场所.结合一道高考立体几何题的展示，以多个思维视角的切入来解题，剖析巧妙的技巧方法与策略应用，指导高考复习备考. 关键词：立体几何；四棱锥；面积；向量；三余弦定理历年高考数学立体几何试题是基于数学课程标准，借助立体几何中的基础知识与基本能力等，合理创设立体几何模型，结合各形式问题的设置来
解题天地 | 2022年高考全国卷第14题解法的五个视角

解题天地 | 2022年高考全国卷第14题解法的五个视角

摘要：对一个数学问题能够从多角度、多视角去探究，有利于我们能切实掌握问题的本质内涵，提高我们灵活解题的能力. 关键词：切线定义;两直线的夹角的斜率计算公式;共交点直线系;四点共圆（2022年高考全国卷第14题）写出与圆x2+y2=1和（x-3）2+（y-4）2=16都相切的一条直线的方程. 本题是求两个圆的公切线方程，那么首先要确定两个圆的位置关系是相离、相交还是相切（分内切和外切），进而
解题天地 | 一道不易分离变量的二元变量最值问题解法探究

解题天地 | 一道不易分离变量的二元变量最值问题解法探究

存在约束关系的二元变量最值的题，是一种常见的题型，一般情况下都可以用公式法、消元法、导数法等求其最值.但是对有约束条件但不易分离变量的二元变量最值问题上述几种方法都不适用，需要我们另辟蹊径，本文中以一道这样的题目为例，赏析它的几种不同的解法，体会这种题型存在的解题规律. 例（江苏省“百校大联考”高三年级第一次考试）已知正实数x，y满足xy（x－y）=4，则x+y的最小值为. 思路一：采用换元
解题天地 | 关注知识交汇 “圆”来并不简单

解题天地 | 关注知识交汇 “圆”来并不简单

摘要：基于《中国高考评价体系》提出的综合性的要求，文章从福建省部分地市2023届第一次质检第8题谈起，探析解析几何中几类圆锥曲线与圆交汇的问题，分析求解策略. 关键词：知识交汇；圆；求解策略研究近几年高考数学试题，不难发现在解析几何的考查中，圆一般出现在选择题或填空题中，经常通过与其他圆锥曲线交汇的形式进行考查.2023届福建省质检第8题即为双曲线与圆交汇的问题，体现了综合性与创新性，是高三
解题天地 | 消元处理，整体代换，巧妙构建：双变量问题的破解技巧

解题天地 | 消元处理，整体代换，巧妙构建：双变量问题的破解技巧

摘要：涉及“双变量”或“双参”的综合应用问题是高考数学压轴题中一类基本应用类型，合理总结与归纳破解此类问题的技巧方法与解题思路是关键所在.结合实例，就破解此类问题的消元处理、整体代换、巧妙构建三种常用技巧方法加以剖析，助力师生的数学教学与学习以及解题研究. 关键词：双变量；消元；整体；同构；函数；不等式近年的高考数学试题中经常涉及“双变量”或“双参”的相关问题，此类问题主要涉及函数与导数、不
解题天地 | 2024年高考数学新高考Ⅰ卷第13题的探究

解题天地 | 2024年高考数学新高考Ⅰ卷第13题的探究

涉及曲线的切线问题，是导数的几何意义与平面解析几何等相关知识的融合，契合高考命题“在知识交汇点处命题”的理念，是高考中比较常见的一类重点与热点问题.特别是涉及两条及以上曲线（主查两条曲线）的公切线问题，新颖度高，创新性强，背景简单易懂，形式复杂多变，求解形式多样，能够有效考查学生的“四基”以及突出学生的“四能”等，凸显试题的选拔性与区分度，倍受各方关注. 1 真题呈现高考真题若曲线y=ex
解题天地 | 挖掘代数式结构，创新构造法应用

解题天地 | 挖掘代数式结构，创新构造法应用

摘要：含参不等式恒成立下的综合问题，是新高考数学试卷中一类考查数学“四基”与“四能”的重要应用场景，场景新颖，知识交汇，内涵丰富，解法灵活.结合一道高考模拟题，就含参不等式恒成立问题中的参数取值范围的求解及其应用，总结解题技巧，归纳方法策略，指导师生的数学教学与学习以及解题研究. 关键词：不等式；最值；构造；分类讨论；性质含参不等式恒成立问题，融入含参场景下的函数、方程或不等式等的综合应用，
解题天地 | 巧构特殊三角模型，妙解抽象函数问题

解题天地 | 巧构特殊三角模型，妙解抽象函数问题

摘要：合理构建特殊函数模型是解决抽象函数综合应用问题的一种比较常用的技巧与策略.结合实例，合理利用问题的应用场景，从问题实质、公式特征、函数特征等方面巧妙构建三角函数特殊模型来解决抽象函数问题，归纳总结解题技巧与策略，指导数学教学与复习备考. 关键词：三角函数；抽象函数；特殊化；模型；应用抽象函数及其综合应用问题，是近年高考数学试卷以及各级各类模拟考试中频频亮相的一类热点与难点问题.巧妙构造
解题天地 | 依托条件等式的设置，探求部分代数式最值

解题天地 | 依托条件等式的设置，探求部分代数式最值

在探求代数式的最值（或取值范围）问题时，经常会碰到一类依托题设条件中等式，进而确定题设条件中等式的“部分代数式”的最值（或取值范围）问题，成为问题创新设置与应用中比较特殊的一种场景，是一类创新新颖的综合应用问题.此类问题，往往基于一次线性代数式、二次代数式以及多选题场景中的代数式等几类常见的最值（或取值范围）的确定来设置，结合实例加以剖析与应用，抛砖引玉. 1 一次线性代数式的最值（或取值范围）
解题天地 | 应用场景巧创设，函数问题妙同构

解题天地 | 应用场景巧创设，函数问题妙同构

摘要：同构是解决数学问题中比较特殊的一种思维方式，是构造法的一种特殊技巧，在历年高考数学命题中都有其“影踪”，倍受命题者的青睐.结合不同的应用场景与条件创设，以不同的方式来实现函数问题的巧妙同构，借助实例剖析，归纳总结同构应用的常见类型，以及解题技巧与方法，指导数学教学与复习备考. 关键词：函数；同构；变量；恒成立；不等式在解决一些函数与导数的综合应用问题时，经常借助题设条件中的代数关系式、
教师发展 | 源于一道错题的生成性教学

教师发展 | 源于一道错题的生成性教学

摘要：真实记录由一道错题引起的，在备课过程中、上课过程中、课后研究中、两周后的考试中的生成性教学，阐述它们生成的原因、过程和结果，并收获了高考的意外之喜. 关键词：错题；生成性；教学生成性教学的概念有多种描述，不同的教师有不同的理解.本文中认为，生成性教学是指教师根据教学过程中出现的信息和问题，及时调整教学思路和教学行为，积极引导教学活动深入持久地进行下去，生成新的超出原计划的教学流程，完成
教师发展 | 六点搞定课堂情境与问题创设的有效性

教师发展 | 六点搞定课堂情境与问题创设的有效性

摘要：创设情境、问题驱动、合作探究、经历过程已经成为新课标数学教学的理论共识.但具体到课堂实践中，如何真正有效实施？本文中以一节课的实施过程为线索，提出了“从单元教学入手，整体理解教材；从核心概念深入，提炼基本问题；从两个维度切入，体验发现过程；从学生认知着手，呈现教育形态；从导问环节精进，追求有效引导；从活化练习拓展，构建真实问题”六点策略，以发展学生核心素养. 关键词：情境；问题；实施策略
教师发展 | 渗透数学抽象素养的三角函数同角关系教学策略探究

教师发展 | 渗透数学抽象素养的三角函数同角关系教学策略探究

摘要：通过借助单位圆作出几何解释、引导学生利用整体换元思想以及充分发挥几何直观方法的价值，提出了一些教学思路.此外，还提出了三个具体的教学策略，即重视相关公式的记忆、加强热点题型的训练、重视多媒体教学工具. 关键词：数学抽象；三角函数；同角关系；教学策略高中数学作为基础学科，其核心素养的培养一直是教育工作者关注的重点.《普通高中数学课程标准（2017年版）》提出了数学抽象作为核心素养之一，帮
教师发展 | 结合2024年高考题谈函数概念与性质的复习

教师发展 | 结合2024年高考题谈函数概念与性质的复习

函数的概念与性质不仅是函数学习的起点，也是解题的关键所在.只有真正掌握了这些基本内容，在遇到复杂的函数问题时，才能迅速找到切入点，有效地解决问题.因此，学生要对函数的概念与性质给予足够的重视，认真学习、反复练习，确保能够熟练掌握和灵活运用.教师通过对高考数学函数概念与性质试题的研究，能够为实际教学带来一些有益的思考和针对性启示，促进教学质量的提升. 1 高考数学真题中函数题目的特点 1.1 题
教师发展 | “三新”背景下的解题教学

教师发展 | “三新”背景下的解题教学

在新教材、新课程、新高考的“三新”背景下，高中数学课堂的教学更加关注知识的发生与发展过程，基于此过程中数学思维品质的提升与数学关键能力的提高，课程观与作业观需在一定程度上转变与创新. 1 问题变式的深度在教学过程中，为帮助学生达成学习目标，往往需要从问题变式中依次提升难度，评估学生的知识掌握情况与思维发展水平，以真正实现解题感悟. 例1 （2024年河北省部分示范性高中高三下学期一模数学试
教师发展 | 新发现的“三垂足定理”新的证明

教师发展 | 新发现的“三垂足定理”新的证明

文[1]遵循原始的发现过程，给出了笔者独立发现且命名为“三垂足定理”的分类证明，而今另辟蹊径，又找到定理新的证明，且对定理的表述有所改进. 先重温圆锥曲线的统一方程：如图1，过点M作MN⊥准线EG交于点N，设F为相应于准线的焦点，e为离心率，则M∈{M｜|FM|=e|MN|}. 取过焦点F且与准线垂直的直线为x轴，点F（O）为坐标原点，建立平面直角坐标系. 设点M的坐标为（x，y），则|

2023年新高考全国Ⅱ卷第22题探究
多角度拓思维研一题通一类
数学史融入高中数学课堂的实践探讨
新人教版高中数学教材中一道三角函数应用题的商榷
基于核心素养的高三数学复习课单元教学设计策略
透视高考真题关注数学阅读
高中数学建模素养培养案例分析
动态与静态的巧妙融合：一道抛物线题的破解
教学聚焦，“图”谋天下
情境创设，概念教学
一节探究抛物线性质“y1y2=-p2”的专题讨论课
圆锥曲线综合探究类题型赏析
三角形面积公式的向量形式及其应用
“局部缩小”在不等式恒成立问题中的应用
例谈充分性在解题中的应用
全概率与贝叶斯公式解题策略探究
揭示知识本质提升核心素养
二次函数的图象性质与零点分布
巧借特殊思维，妙破解析几何
数学解题教学中解题过程严谨性及规范性探究
2024年高考题中的高阶思维能力考查
特殊思维巧应用，高考真题妙解答
抓住本质，从一般到特殊命制试题
一道高中数学典型例题的素养分析及命题启示
一道高考解析几何压轴题的探究
2023年新高考Ⅰ卷第17题的多解、溯源、变式
岁岁年年“题”不同，年年岁岁“解”相似
三角搭台导数唱戏：探究与三角函数交汇的函数导数问题
重心巧创新，向量妙“包装”
挖掘问题本质，实现“一题多解”
特殊值法巧用，高考真题妙解
棱台场景创设，线面角求解
含参函数奇偶性，方法与素养齐飞
存在性判定，思维性应用
问题深入挖掘，思维合理发散
拓展数学思维，总结解题技巧
把握三次函数本质，巧思妙解综合应用
巧思维展开，妙方法应用:一道椭圆解答题的探究
2024年高考数学新高考Ⅱ卷第15题的探究
深挖命题内涵，多解变式应用
巧思维开拓思路，妙应用变式拓展
“数”“形”思维切入，位置关系突破
2023年高考数学全国甲卷理科题11的探究
2022年高考全国卷第14题解法的五个视角
一道不易分离变量的二元变量最值问题解法探究
关注知识交汇 “圆”来并不简单
消元处理，整体代换，巧妙构建：双变量问题的破解技巧
2024年高考数学新高考Ⅰ卷第13题的探究
挖掘代数式结构，创新构造法应用
巧构特殊三角模型，妙解抽象函数问题
依托条件等式的设置，探求部分代数式最值
应用场景巧创设，函数问题妙同构
源于一道错题的生成性教学
六点搞定课堂情境与问题创设的有效性
渗透数学抽象素养的三角函数同角关系教学策略探究
结合2024年高考题谈函数概念与性质的复习
“三新”背景下的解题教学
新发现的“三垂足定理”新的证明

过往期刊

更多

中学数学·高中版
2024年11期
中学数学·高中版
2024年10期
中学数学·高中版
2024年09期
中学数学·高中版
2024年08期
中学数学·高中版
2024年07期
中学数学·高中版
2024年06期
中学数学·高中版
2024年05期
中学数学·高中版
2024年04期
中学数学·高中版
2024年03期
中学数学·高中版
2024年02期
中学数学·高中版
2024年01期

猜你喜欢

时代英语·高一
2024年08期
时代英语·初中
2024年06期
高中数理化
2024年21期
发明与创新·上旬刊
2024年11期
语文世界(中学版)
2024年11期
发明与创新·下旬刊
2024年11期
中学生数理化·高二数学
2024年11期
少男少女·小作家
2024年11期

Copyright © 2017 龙源数字传媒集团京ICP备060024号
Dragonsource.com Inc. All Rights Reserved
IP:3.145.93.227

苏州工业园区教育局电子阅览室

首页
全部分类
排行榜
客户端下载

登录
个人中心我的收藏退出登录
简体 / 繁体

苏州工业园区教育局电子阅览室

忘记密码新用户

新用户注册

已有账户

注册成功

修改电子邮件