全部分类/
中学教育/
中学数学·高中版

中学数学·高中版

2024年05期

扫码免费借阅

目录

快速导航

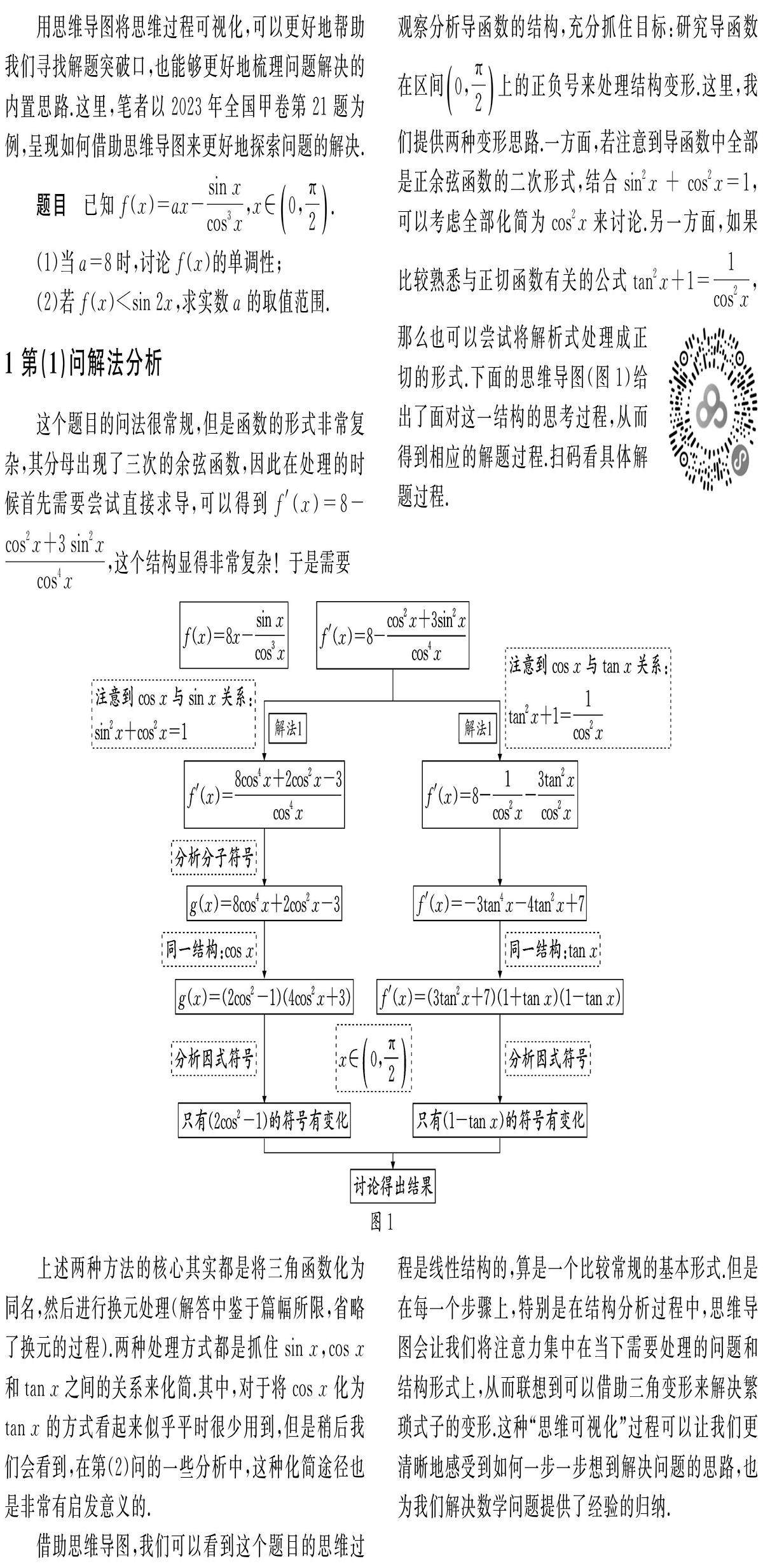
讲题比赛 | 借助思维导图将思维“可视化”，探寻解题轨迹

讲题比赛 | 借助思维导图将思维“可视化”，探寻解题轨迹

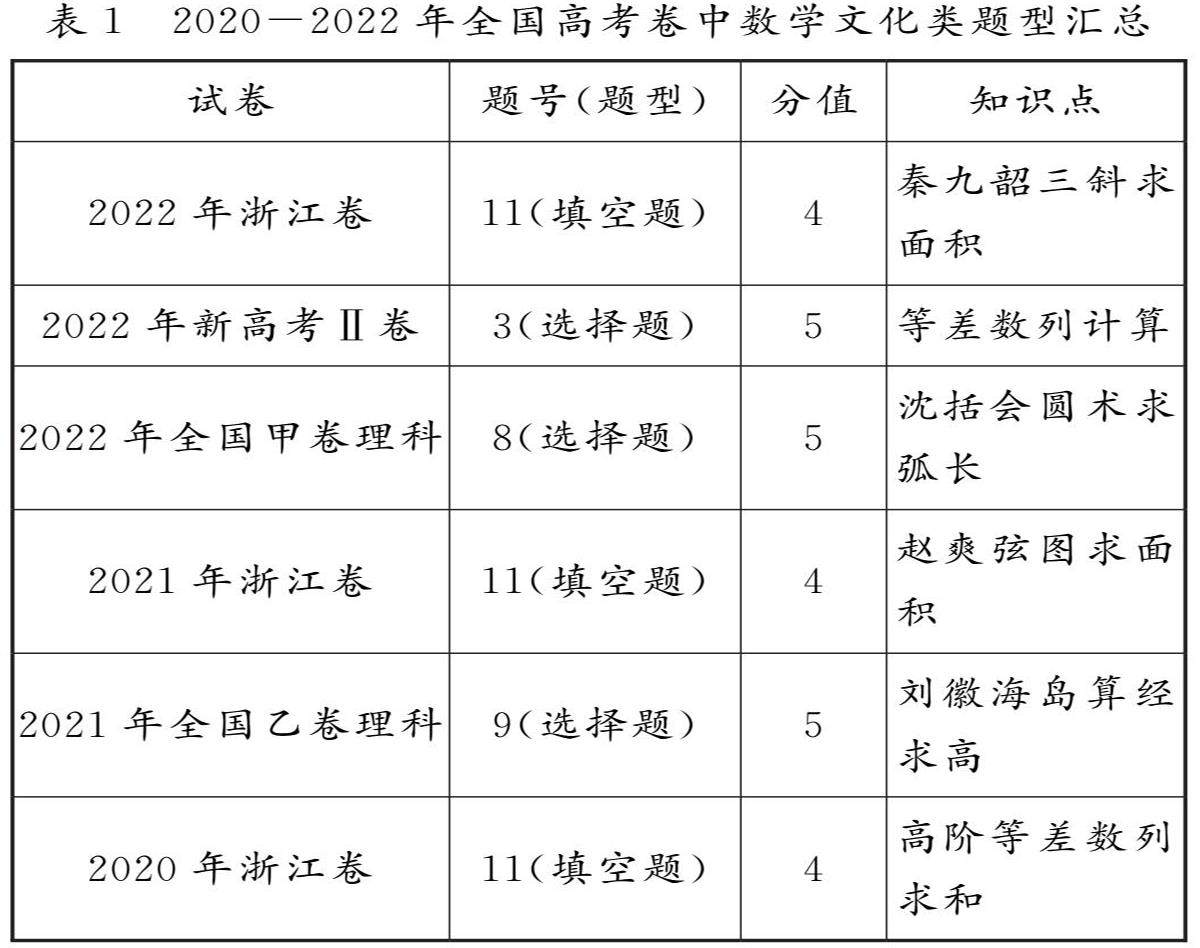
用思维导图将思维过程可视化，可以更好地帮助我们寻找解题突破口，也能够更好地梳理问题解决的内置思路.这里，笔者以2023年全国甲卷第21题为例，呈现如何借助思维导图来更好地探索问题的解决. 题目已知f（x）=ax－ sin x cos3x ，x∈ 0， π 2 . （1）当a=8时，讨论f（x）的单调性；（2）若f（x）<sin 2x，求实数a的取值范围. 1 第（1）问解法分析
数学教育 | 重数学文化涵泳为学科素养赋能

数学教育 | 重数学文化涵泳为学科素养赋能

2022年自主命题的浙江卷在第11题中要求以秦九韶三斜求积公式求三角形面积，浙江卷2020-2022年高考中每年都在第11题出现数学文化类题型，数学文化的渗透和领会，是数学教学中不可或缺的一部分，也是培养学生数学学科核心素养文化价值的有力体现.2019普通高中数学教材人教版A版（以下简称“新教材”）在课程内容上增设了“阅读与思考”“探究与发现”等拓展性栏目，这些栏目内容涵盖了国内外数学发展历史中的
数学教育 | 聚焦数学结构之美挖掘文化育人价值

数学教育 | 聚焦数学结构之美挖掘文化育人价值

目前高中各门学科中，数学已经成为高中最难学的学科之一，尤其对于思维偏文的学生.笔者从事高中数学教学已有十余年，发现众多的数学课堂，总有部分学生提不起对数学的兴趣，或者感觉数学枯燥乏味.于是，笔者提出，数学课堂能否也有欢声笑语？能否让数学学习变得轻松简单，更具有可操作性？这需要改变我们的思维方式和教学方式，让难的数学问题通过分解，变成简单的问题，做到复杂问题简单化；而简单的问题需要讲得接地气、贴近生
数学教育 | 用理性精神让数学与物理适度融合

数学教育 | 用理性精神让数学与物理适度融合

在新课程、新教材、新高考的“三新”背景下，“注重在数学知识网络的交汇处设计试题”，已经成为近年新课标高考数学试题的创新特色之一，更是深度契合高考数学命题的基本指导思想.特别地，对数学与物理这两个跨学科适度融合方面的尝试与创新，成为众多跨学科适度融合方面最为典型的一类基本考点，备受各方关注. 1 借助函数模型阐述物理现象问题例1 如图1，某炮兵从地平面A处发射一枚炮弹至地平面的另一处B，假设炮
数学教育 | 新人教A版与北师大版高中数学教材对比

数学教育 | 新人教A版与北师大版高中数学教材对比

摘要：高中数学教材版本多样，其中新人教A版和北师大版应用广泛，文章以“平面向量及其应用”章节为例，具体对两个版本教材的体系结构、栏目设置、新知呈现方式、例习题难度等四个方面进行分析，根据研究结果提出教学建议. 关键词：教材对比；平面向量；教学建议教材是实施课程改革的物质载体，现行的高中数学教材版本多样，每个版本都有自己的编写特色.对比研究不同版本教材能够使教师把握教学方向，多方面了解知识内
数学教育 | 依托教材，返璞归真：立体几何中的截面问题

数学教育 | 依托教材，返璞归真：立体几何中的截面问题

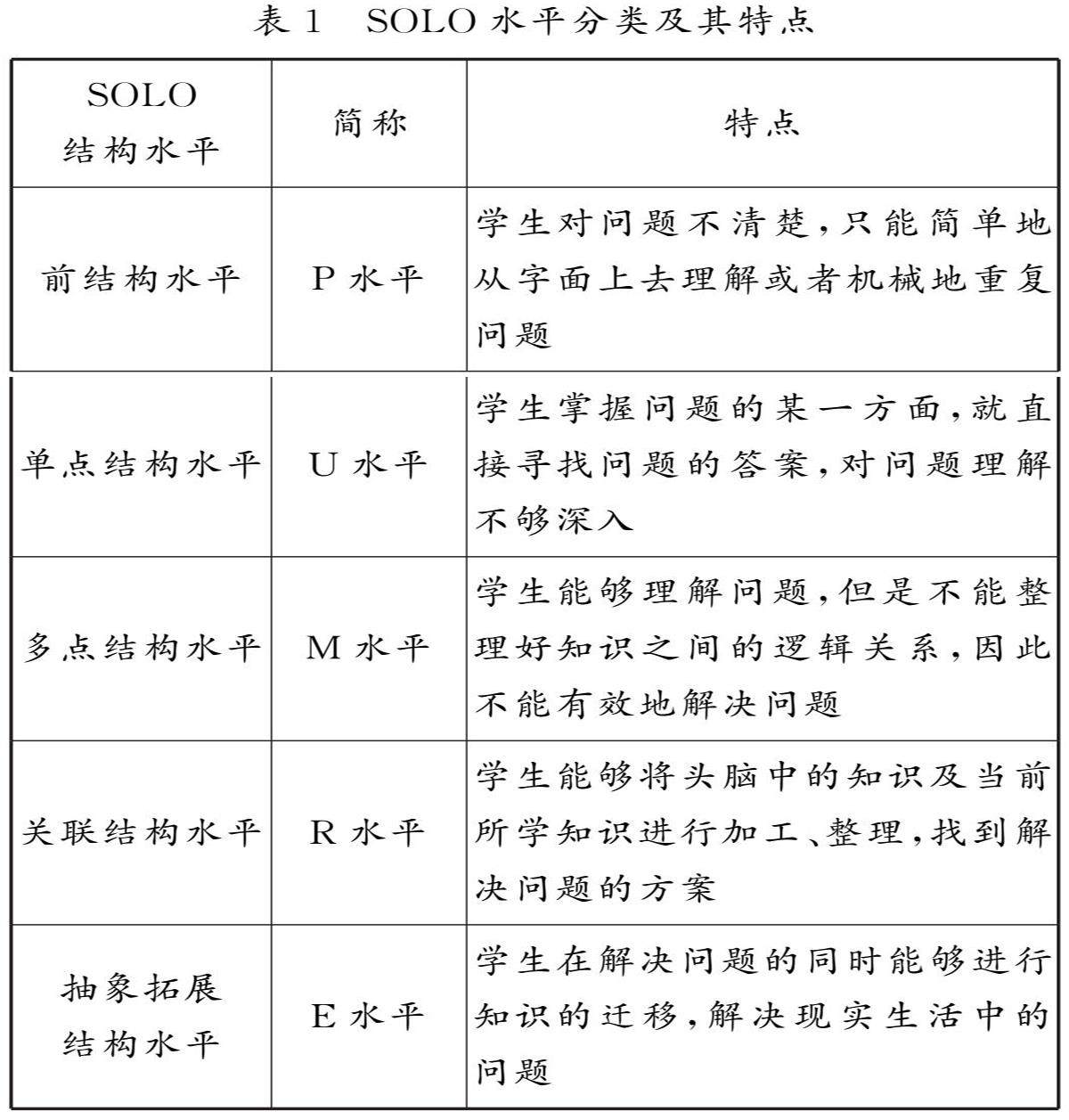
在处理立体几何综合问题时，经常会碰到截面问题，其是基于借助一个平面（或不共线的三点、一直线与该直线外一点、两平行直线等）去截对应的空间几何体，进而所创设的问题场景及其相应的应用问题.此类截面问题，合理构建“二维”与“三维”之间的联系，从而构建平面几何与立体几何的升维与降维思想，一直是高考数学命题中比较常见的一类基本考查方式，备受关注. 1 依托教材，构建概念 1.1 链接教材问题（人教A
教法探索 | SOLO分类理论指导下的教、学、评一体化设计

教法探索 | SOLO分类理论指导下的教、学、评一体化设计

摘要： SOLO分类理论为复杂的学习过程提供了一个通用框架，在其理论指导下的教学设计能够对学生学习质量进行客观、可观察的评价，可以有效避免“教学设计全凭经验与感觉”“课时目标不准确、不具体、不可评”“学习活动与学习目标两张皮”“教、学、评一致性不匹配”等不合理现象.本文中针对“充分条件与必要条件”内容特点及其教学现状，结合SOLO分类理论，进行教、学、评一体化设计. 关键词：SOLO分类理论;教
教法探索 | MPCK视角下的“基本不等式”单元教学

教法探索 | MPCK视角下的“基本不等式”单元教学

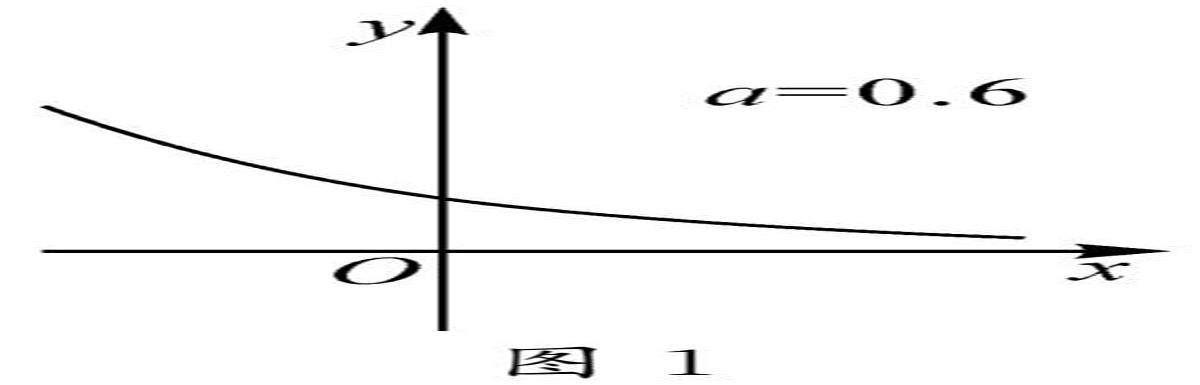
摘要：以人教A版（2019年版）教材中“基本不等式”为例，从MPCK视角，对大单元教学设计教师所需的专业素养进行探讨，探究学生数学核心素养和落实学科育人的途径. 关键词：MPCK；基本不等式；大单元教学 1 问题的提出新课程标准要求以培养学生的数学核心素养为出发点和落脚点，强调以“学科大单元”为载体，多层次、多方式、多角度在教学活动中发展学生的“四基”“四能”.在教学实践中落实上述要求，
教法探索 | 利用GGB软件辅助高中数学新教材函数教学

教法探索 | 利用GGB软件辅助高中数学新教材函数教学

摘要：函数是数学中一个重要的概念，也是新教材高中数学教学的重点和难点.如果教师能巧妙地利用函数图象将抽象的问题转化为直观的图形，则可以帮助学生有效地理解函数，也可以大大降低学习函数的难度.利用GGB软件展示一些常见的函数图象，让学生充分进行观察和思考，并总结出相关函数的图形的特征.这样就可以有效辅助函数的教学工作，从而相对轻松地突破高中阶段的重点教学内容. 关键词：函数；GGB软件；辅助函数
教法探索 | 高中数学主题教学设计应把握四个关键点

教法探索 | 高中数学主题教学设计应把握四个关键点

摘要：高中数学教学的主要目的是培养学生的数学能力和数学核心素养，因此需要充分结合教学目的及落实立德树人的根本任务来进行教学设计.同时，在教学设计的过程中要有效把握教学内容的整体性、教学目标的结构性、教学过程的层次性以及教学评价的发展性这四个关键点.本文中以“函数单调性”主题教学设计为例，对高中数学教学设计的要点进行了分析. 关键词：高中数学；教学设计；关键点；主题教学；函数的单调性新课标明
教法探索 | 迈向深度学习，优化复习效益

教法探索 | 迈向深度学习，优化复习效益

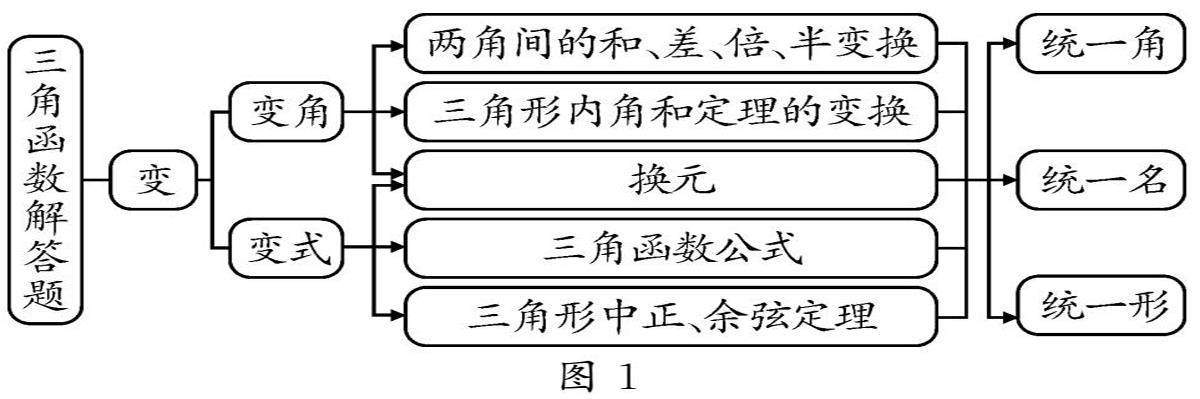
“一题多解”是高中数学课堂教学与学习中比较常用的一种基本手段，更是高考复习中非常有效的一种教学方式.借助“一题多解”，可以有效引领复习，夯实“四基”，进而全面克服学生解题中的思维定势，有效发散数学的灵动思维，培养学生思维的灵活性与创新性，这对复习备考是非常有益的.而借助“一题多解”，能更加充分体现学生对整体知识的理解掌握情况，以及更加灵活的应用能力，也能更加有效地提升学生的“四能”，达到高效复习的
教法探索 | 创新思维，优化策略

教法探索 | 创新思维，优化策略

摘要：提升高考数学二轮复习的质量与效益，成为复习备考中最为关键的一个基本环节.依托高考数学二轮复习，从不同层面切入，创新复习思维，优化复习策略，帮助学生构建更加全面细致的数学知识网络体系，有效提升数学能力和核心素养. 关键词：创新；思维；策略；二轮复习；建议高考数学二轮复习，是在一轮复习中构建较为完备的数学知识结构与思想方法体系的基础上，旨在引领学生通过课堂教学与练习训练等形式，借助数学知
教法探索 | 基于“三新”背景，高考备考建议

教法探索 | 基于“三新”背景，高考备考建议

摘要：在“三新”背景下，高考命题倡导改革与创新，关注考生的“四基”与关键能力等，这就给高考复习与备考提出更高的要求.以“三角函数”为例，合理回归概念，巧妙突出重点，借助“一题多解”，坚持错题整理等，有效落实复习内容，强化解题思维，拓展技巧方法，提升复习备考的质量. 关键词：新教材；新课程；新高考；备考；三角函数在新教材、新课程、新高考的“三新”背景下，高考复习与备考显得更加重要，成为复习阶
教法探索 | “概率统计”的复习备考建议

教法探索 | “概率统计”的复习备考建议

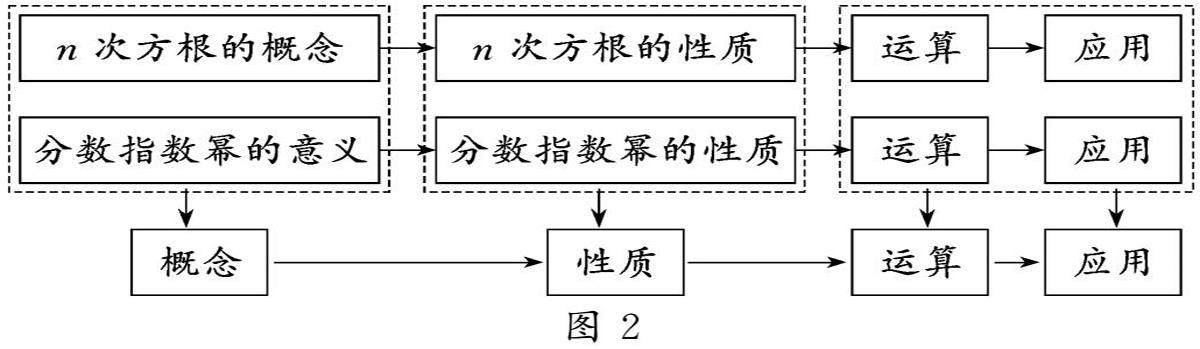
摘要：作为高考中的主干知识之一，概率统计部分的复习备考是高考复习中的一个重要环节.通过数学阅读能力培养、数学概念公式理解、数学思想方法提炼、知识内涵与解题规范、未涉及知识教学复习等层面的展开，剖析复习备考建议，全面提升数学能力与培养核心素养，优化复习备考效益. 关键词：概率；统计；高考；备考；复习建议概率统计（含计数原理、排列组合与二项式定理等）模块知识是新高考数学试卷中的一个重要考查知识
教法探索 | 基于深度学习渗透核心素养

教法探索 | 基于深度学习渗透核心素养

深度学习是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程[1]. 数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析[2]. 如何开展教学才能更好地推动学生深度学习、发展学生核心素养呢？教师需要在把握数学本质的同时，兼顾学生的思维规律与教学的基本规律，创设恰当的情境，让学生围绕揭示本质的问题展开深度学习.笔者设
教法探索 | 课例：函数的奇偶性

教法探索 | 课例：函数的奇偶性

摘要：奇偶性是函数的重要性质.“函数的奇偶性”的教学按照研究函数性质的一般方法，通过问题串的形式，再适当融入数学文化来组织，以帮助学生更好地完成对“奇偶性”概念的建构和理解. 关键词：函数的奇偶性；问题串；数学文化 1 教学内容分析 “函数的奇偶性”是人教A版数学必修第一册第三章第二节的内容.一方面，函数的奇偶性是继函数的单调性后的又一重要性质，它延续了研究函数单调性的方法；另一方面，它也
教法探索 | 思维导图在整体性教学中的应用实践

教法探索 | 思维导图在整体性教学中的应用实践

摘要：整体性教学为学生营造了更多自主探究的空间，学生可以获得更多的机会去思考、去探索、去实践，以此加深对相关知识的理解，建构个体完善的知识体系.在日常教学中，教师要重视引导学生运用思维导图将知识、思想方法等联系起来，逐步培养整体观，提高数学学习效率. 关键词：整体性教学；思维导图；学习效率数学是一门逻辑性较强的学科，但受学生认知水平、思维能力等因素的影响，这些逻辑连贯的数学知识可能分散于不同
教法探索 | “生本”理念下精彩习题课堂的建构

教法探索 | “生本”理念下精彩习题课堂的建构

摘要：在高中数学习题课上，教师应结合教学实际不断创新教学手段和教学模式，充分发挥学生的主体价值，让学生成为习题课真正的主人.在具体实施过程中，教师要做启发型和探究型的老师，要重视呈现学生的思考过程，并鼓励学生从不同角度分析和解决问题，以此帮助学生积累丰富的解题经验，切实提高学生解题能力，提升学生数学素养. 关键词：习题课；主体价值；解题能力习题课是数学教学的重要课型，它既可以检测学生知识、技
教法探索 | 借助高质量提问打造高品质课堂

教法探索 | 借助高质量提问打造高品质课堂

摘要：课堂提问作为师生对话的重要形式，其在激发学生潜能、唤醒学生思维、提升学生数学素养等方面发挥着积极的作用.在高中课堂教学中，教师要从教学实际出发，结合课堂生成提出高质量的问题，让学生在深度对话中不断积累活动经验，完善认知结构，以此提升教学品质和学习质量. 关键词：课堂提问；教学品质；学习质量课堂是师生互动交流的平台，课堂教学离不开师生的对话.若课堂上没有对话，课堂教学就成了教师的独角戏，
学生学习 | 与时俱进时代特色，关注经济科技生产

学生学习 | 与时俱进时代特色，关注经济科技生产

近年高考数学命题围绕“立德树人”的根本目标，在考查学生“四基”的基础上，坚持数学思想性、科学性与应用性等方面的融合与和谐统一.而数学命题的设置，可以在此精神指导下，创设一些具有创新教育意义的数学场景，融入数学知识与数学应用，利用高考“指挥棒”合理引导数学教学与数学学习，引导学生增强社会责任感与使命感，教育并引领学生树立正确的人生观、价值观、世界观. 1关注科学进步与技术创新 2021年高考数学
学生学习 | 从一道2023年高考题谈二面角的求法

学生学习 | 从一道2023年高考题谈二面角的求法

摘要：求二面角的大小是高数学中的一个重点和难点问题，也一直是历年高考的高频考点，重点考查逻辑推理、直观想象和数学运算等数学学科核心素养.但是大部分学生仍然畏惧这类题型或者解此类题的方法非常单一，本文中通过“一题多解”来探究二面角的求法，帮助学生掌握解决此类题的方法，领悟解题过程中蕴含的数学思想. 关键词：二面角；核心素养；数学思想 1真题再现题目（2023年新课标全国Ⅱ卷）如图1，三棱锥A
学生学习 | 泰勒公式与高考试题

学生学习 | 泰勒公式与高考试题

摘要：如何提升学生解导数压轴题的能力，是高三复习过程中一个艰巨而又重要的课题.本文中从历年高考导数压轴题出发，深入探究导数与泰勒公式之间的渊源，揭示了导数压轴题的泰勒公式背景，利用泰勒公式的特殊形式，归纳了几种常见的重要不等式，总结了导数压轴题的几种类型，并提出了策略性的思考. 关键词：泰勒公式;高考试题；解题策略；考题研究泰勒（Taylor）以微积分中将函数展开成无穷级数的定理而著称于世
学生学习 | “三叉戟”模型在解析几何中的深度应用

学生学习 | “三叉戟”模型在解析几何中的深度应用

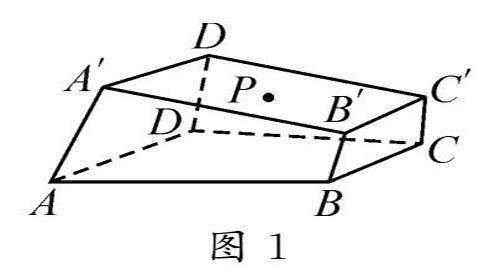
摘要：在研究高考试题时，发现平移齐次法是解决圆锥曲线综合问题的好方法，但是平移齐次常见的应用是解决两直线斜率和（或积）为定值的问题，且不知道怎样的试题适合利用平移齐次法.本文中归纳了一个模型——“三叉戟”模型，只要是过定点的两条直线与圆锥曲线有两个交点，这三点构成三角形，都可以运用平移齐次；总结了怎样代入构造齐次式的方法，并且首次利用平移齐次法解决了2022年浙江高考题中求弦长的最值问题及202
学生学习 | 重构学习单元，创新学习指导

学生学习 | 重构学习单元，创新学习指导

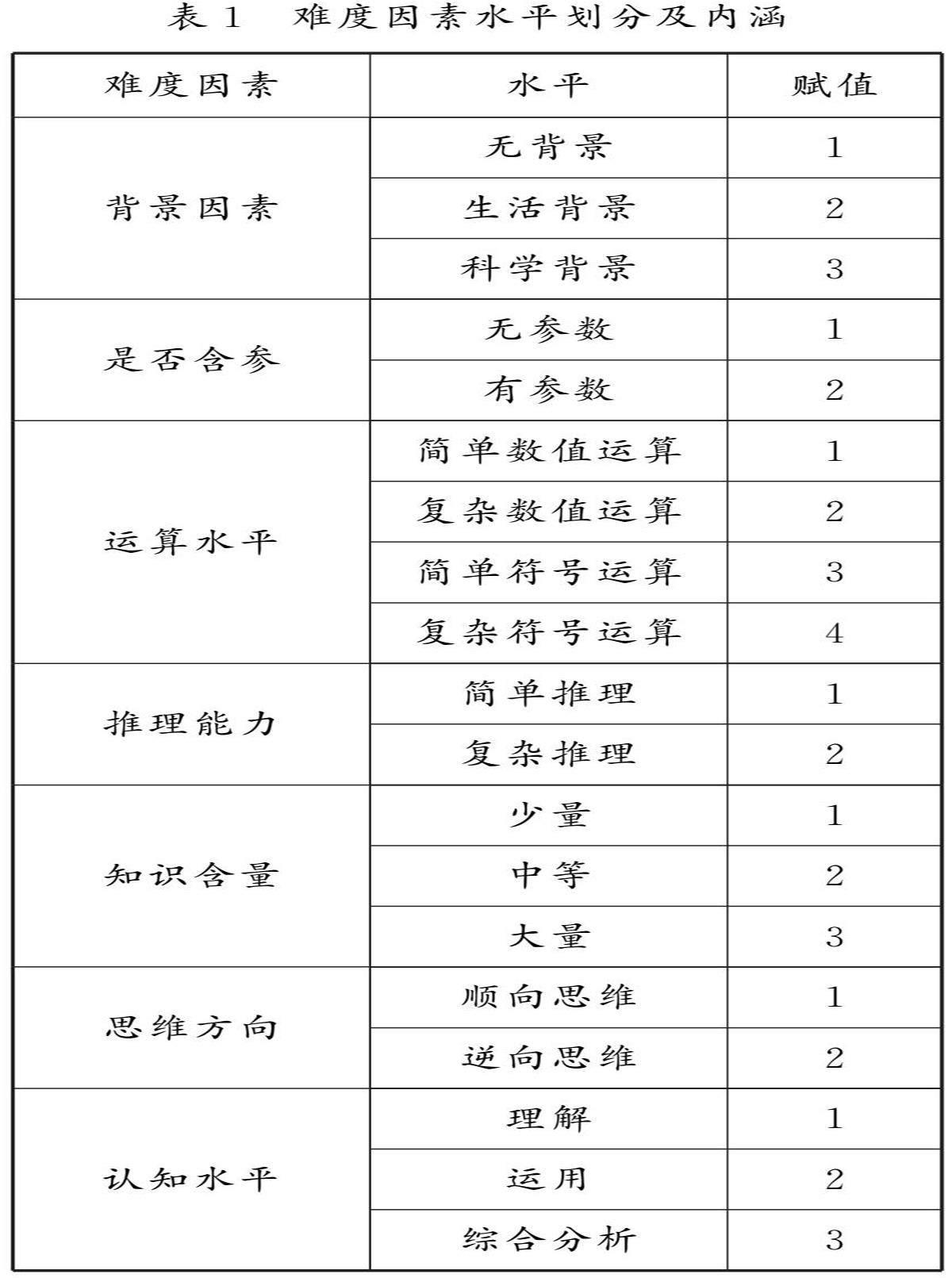
在新教材、新课程、新高考的“三新”背景下，立体几何中空间几何体模块知识的高考命题与综合应用更加新颖创新，特别是有关空间几何体截面知识的应用，成为高考数学命题的一个热点与亮点，备受各方关注.涉及空间几何体的截面问题，源于高中教材，依托教材合理构建截面概念；在此基础上，强化截面的本质与内涵，增加平面几何与立体几何等相关知识之间的联系；彰显与截面相关知识的应用，充分体现数学意识与数学思维能力；强化截面的
评价透视 | 高考数学“概率与统计”试题的特点及其教学启示

评价透视 | 高考数学“概率与统计”试题的特点及其教学启示

1背景 “概率与统计”是高中数学四大主要课程之一.而高考中“概率与统计”试题形式多变，考查的侧重点和综合难度都有一定的变化，部分一线教师难以把握高考复习方向[1]，因此对全国卷（全国甲卷、乙卷，新高考Ⅰ卷、Ⅱ卷）中“概率与统计”的相关试题进行统计分析，为教学实践提供有效的建议，提醒教师重视“概率与统计”内容[2].为教师开展有效的教学活动提供方向，充分发挥新高考在数学学科教育中的导向作用，以达到
评价透视 | 拾级而上重本质，开拓进取升素养

评价透视 | 拾级而上重本质，开拓进取升素养

2023年全国数学新高考Ⅱ卷顺应高考命题改革，以素养为导向，通过创设多样命题情境，突出对数学关键能力的考查，充分发挥数学学科在人才选拔中的重要作用. 1深化基础考查，指向关键能力《中国高考评价体系》指出，高考以能力为重、知识为基，关键能力是高考重要的考核目标，也是测试和评价的核心指标和因素.数学关键能力是指进入更高层次的学习者，在面对数学学科相关的生活实践或学习探索问题情境时，能有效地提出问
评价透视 | 研读高考试卷的三个层次

评价透视 | 研读高考试卷的三个层次

摘要：研读高考试卷，就是以课标的理念、思想、要求来研读；研读试题，不仅要研读试题的解法，还要研读问题产生的情境，追寻试题的命题背景及思维轨迹，挖掘试题所潜藏的教育资源，引领学生高观点认识试题，认清数学试题的大背景，掌握研究方法，学会在大背景下思考问题，拓展思维. 关键词：初读（读点、读线）;再读（读面、读体、读脉）;三读（读情境、读背景）一份高考试卷，就像一轮月亮. 1层次一：初读如漫步中
评价透视 | 数山探路悟法理学海驾舟求真知

评价透视 | 数山探路悟法理学海驾舟求真知

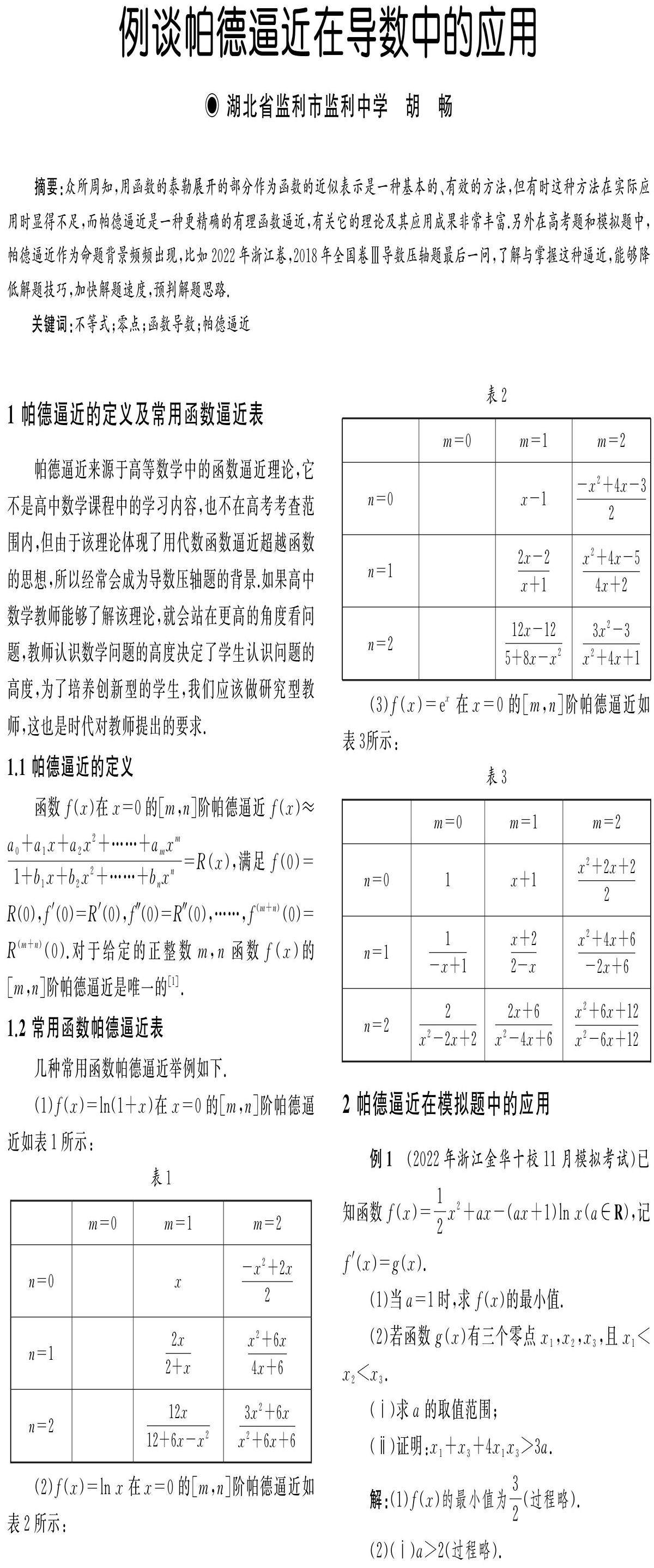
1新题呈现 2023年高中数学命题比赛中，笔者受华南师范大学吴康教授将2022年新高考Ⅰ卷第22题拓展到四个交点情形的启发，通过对高考原题进行改编，命制了如下一道导数压轴题. 已知函数f（x）=axex－b和函数＿＿＿＿有相同的最大值.请在以下的函数①g（x）=axlnx－b，②g（x）=lnxax－b，③g（x）=lnx+ax－b中，恰当地选择其中一个函数，把相应序号填写到横线中，并完成下列
评价透视 | 例谈帕德逼近在导数中的应用

评价透视 | 例谈帕德逼近在导数中的应用

摘要：众所周知，用函数的泰勒展开的部分作为函数的近似表示是一种基本的、有效的方法，但有时这种方法在实际应用时显得不足，而帕德逼近是一种更精确的有理函数逼近，有关它的理论及其应用成果非常丰富.另外在高考题和模拟题中，帕德逼近作为命题背景频频出现，比如2022年浙江卷，2018年全国卷Ⅲ导数压轴题最后一问，了解与掌握这种逼近，能够降低解题技巧，加快解题速度，预判解题思路. 关键词：不等式；零点；函数
评价透视 | 基于数学命题方式，实现问题价值提升

评价透视 | 基于数学命题方式，实现问题价值提升

数学试题的命题，是数学教学过程中一项重要而又严谨的工作，在一定程度上体现数学教师与教研员等对数学基础知识、数学思想方法等的提炼程度，以及自身所具备的一定数学专业水平等，具有一定的技术与技巧.这往往也在一定程度上展示数学教师与教研员等的一项基本能力与水平. 数学试题的命题，往往是一个反复琢磨、不断修改的复杂过程.而这些典型的数学试题，特别是高考真题、竞赛题、模拟题等优秀的试题，往往都不是凭空生造出
解题天地 | 对一道解析几何试题的探究与拓展

解题天地 | 对一道解析几何试题的探究与拓展

1真题呈现解析几何在全国新高考卷中分值占比较大，往往以2个客观题、1个解答题的形式出现，是考查的重点，备受关注.下面我们从一道高考真题说起. 已知点A（2，1）在双曲线C：x2a2－y2a2－1=1（a>1）上，直线l交C于P，Q两点，直线AP，AQ的斜率之和为0.（1）求l的斜率；（2）若tan∠PAQ=22，求△PAQ的面积. 这是2022年全国数学新高考Ⅰ卷的第21题，主要考查
解题天地 | 一道三角最值题的破解与拓展探究

解题天地 | 一道三角最值题的破解与拓展探究

三角函数的最值或取值范围等综合问题，一直是高考中三角函数知识模块的重点与难点之一，可以很好融合三角函数的基本概念、基本公式、三角函数的图象与性质等，以及函数与方程、函数与导数、不等式及其应用等相关知识，思维视角多样，方法技巧多变，是全面考查数学“四基”与数学能力、展示知识交汇与体现方法多样性的一个重要场所，倍受各方关注. 1问题呈现问题（湖北省武汉市武昌区2023届高三年级5月质量检测数学试
解题天地 | 2022年新高考Ⅰ卷第12题函数性质的思考

解题天地 | 2022年新高考Ⅰ卷第12题函数性质的思考

2022年数学新高考Ⅰ卷第12题是关于原函数与导函数的“奇偶性”“对称性”的关系，以及函数图象变换和函数周期性的问题.题目综合性强，难度大.在人教版高中数学新教材中都能看到本题的影子.例如，人教A版高中数学新教材必修第一册第87页“拓广探索”第13题及第214页“拓广探索”第19题.人教A版高中数学新教材选择性必修第二册第5章第3节的节引言说明利用导数能更精确地研究函数的性质.教材中用导数研究函数
解题天地 | 不等式情境，函数性视角

解题天地 | 不等式情境，函数性视角

含参不等式的存在性问题是高考数学试卷中比较常见的一类综合应用问题，经常交汇融合函数与不等式的相关知识，场景变化多端，形式创新多变，是知识综合与创新应用的一个重要载体.此类问题经常借助含参不等式的合理恒等变形与等价转化，综合利用不等式的基本性质转化为函数问题，从函数的视角来分析，借助函数的基本性质、图象等来处理与应用，实现问题的巧妙解决. 1问题呈现问题（山东省新高考联合质量测评2022年12
解题天地 | 多角度探究圆锥曲线中的定值问题

解题天地 | 多角度探究圆锥曲线中的定值问题

摘要：文章对2023年高考数学全国乙卷第20题（圆锥曲线问题）进行解法探究和变式拓展，经过对该题的溯源和剖析，发现其解法的多元性及通用性，并将其推广到更一般的形式，以更好地促进教师的“教”和学生的“学”. 关键词：高考数学;圆锥曲线;一题多解 1真题再现真题（2023年全国乙卷理科数学第20题）已知椭圆C：y2a2+x2b2=1（a>b>0）的离心率是53，点A（－2，0）在C
解题天地 | 切点弦场景创设，定点与动点轨迹

解题天地 | 切点弦场景创设，定点与动点轨迹

切点弦是二次曲线中一类比较特殊的弦，其是由二次曲线外的一点向二次曲线引两条切线，连接两切点的线段.特别对于抛物线中的切点弦问题，更是其中一个具有独特属性的知识点，备受关注. 1问题呈现问题（2024届广东四校高三第一次联考数学试卷·16）过P（m，－2）向抛物线x2=4y引两条切线PQ，PR，切点分别为Q，R.又点A（0，4）在直线QR上的射影为H，则焦点F与H连线的斜率的取值范围是＿＿＿＿
解题天地 | 强化“三思维”，破解三角形

解题天地 | 强化“三思维”，破解三角形

摘要：解三角形问题可以有效沟通初中平面几何与高中相关知识，实现知识的交汇与融合，一直是高考中的基本考点，本文中结合高考真题加以实例分析，从不同思维视角切入，强化破解三角形问题的“三思维”，总结规律，启示教学，指导数学教学与解题研究. 关键词：三角形；正弦定理；余弦定理；坐标；几何解三角形试题一直是历年高考命题的基本考点与热点问题之一，有时以解答题的形式出现，有时以选择题或填空题的形式出现，简
解题天地 | 例谈不等式恒成立求参数范围问题的解题策略

解题天地 | 例谈不等式恒成立求参数范围问题的解题策略

摘要：不等式恒成立求参数范围的问题是高考和各地模拟考试中的热点问题，此类问题形式多样，解决起来有一定困难，本文中通过具体例子探讨此类题型的解题策略，分析其中的思维逻辑. 关键词：不等式恒成立；参数范围；解题策略不等式恒成立求参数范围的问题能够充分联系不等式、函数与方程、导数等知识，有利于考查学生数学运算、逻辑推理、数学抽象等学科核心素养，是高考和各地模考的热点问题.此类问题形式多变、综合性强
解题天地 | 线性规划常见题型及解法例析

解题天地 | 线性规划常见题型及解法例析

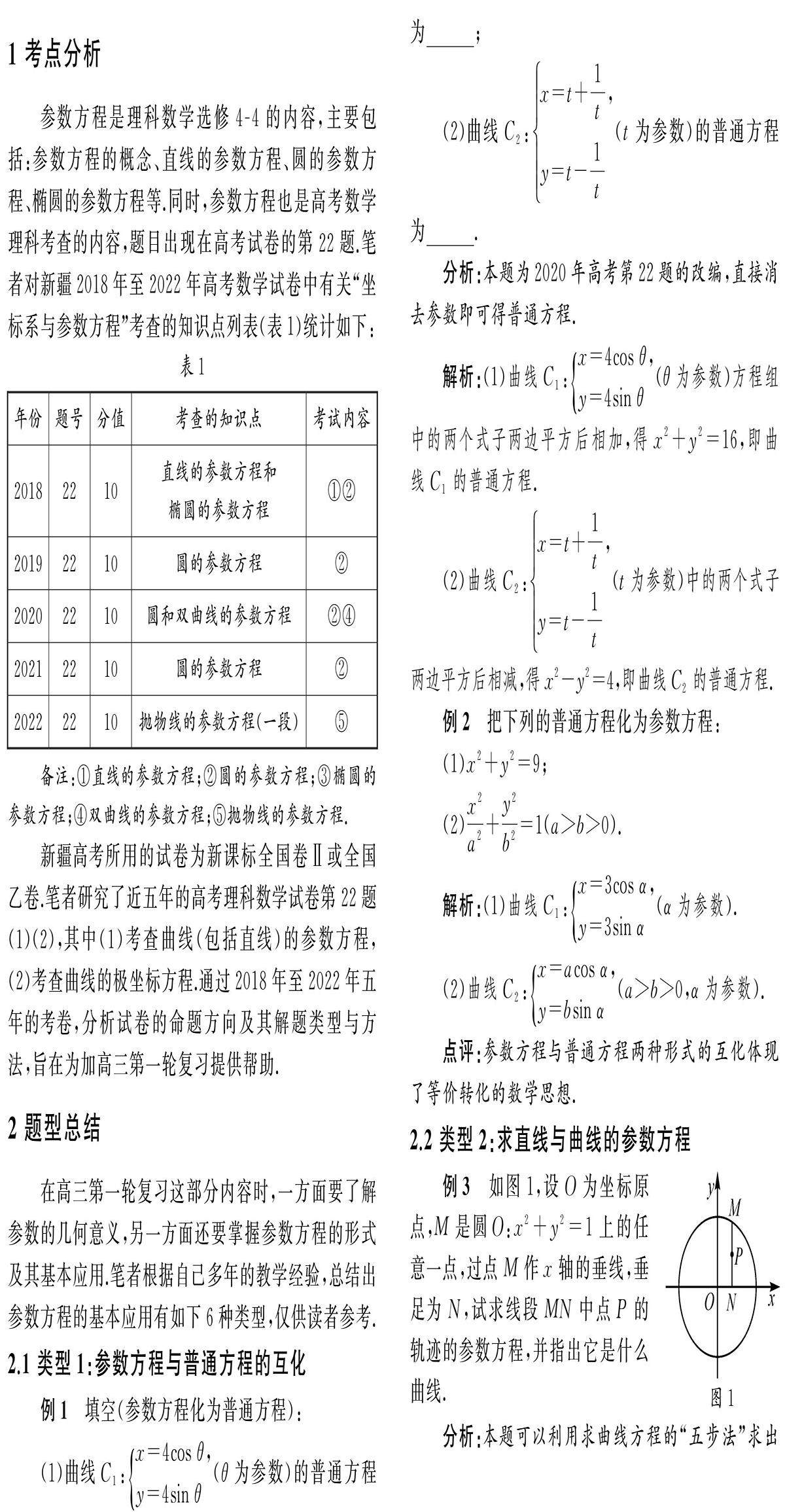
线性规划问题是高考的必考内容和热点之一，主要考查在线性约束条件下的函数最值问题以及应用线性规划的方法解决一些实际问题；内容涉及到了所有题型，其中选择题和填空题的分值占6～8分，解答题中分值高达10～15分，其重要性可见一斑.所以，无论是在平时的学习还是高考备考中，我们都应该注重学习和掌握线性规划知识，强化解题训练，熟知常见题型及解题方法，这样才能在考场上应对自如地获取高分，不断提升自身的数学综合能
解题天地 | “参数方程”的高三数学第一轮专题复习课例

解题天地 | “参数方程”的高三数学第一轮专题复习课例

摘要：“参数方程”是高中数学理科的重点内容，也是理科数学高考的考查内容之一；考试题目出现在试卷第22题（选做题），分值为10分.高考考查的知识点主要包括直线、圆和椭圆的参数方程，在第一轮复习时，要研究高考命题的难度和类型，有针对性地展开复习关键词：参数方程；高三数学;第一轮复习;课例 1考点分析参数方程是理科数学选修4-4的内容，主要包括：参数方程的概念、直线的参数方程、圆的参数方程、椭
解题天地 | 不平移齐次化方法在圆锥曲线问题中的应用

解题天地 | 不平移齐次化方法在圆锥曲线问题中的应用

圆锥曲线问题，由于其侧重考查学生的数学运算、逻辑推理、直观想象等核心素养，是高考数学中一个重要的考点，其中一类以直线的斜率之和或者之积为背景的圆锥曲线问题更是近几年高考中考查的热点.运用平移齐次化方法求解圆锥曲线问题，具有简化计算、提高解题效率的作用，但此法需要平移圆锥曲线或者平移整个坐标系，因此，先要重新绘制图形，且在计算过程中需要左、右或者上、下平移，计算结束后再平移回原来位置，实际书写也
解题天地 | 一道新高考解析几何题的多解探究

解题天地 | 一道新高考解析几何题的多解探究

摘要：解析几何是高中数学最重要的部分之一，长期以来都是高考的重点和难点.在全国广泛推行新课标与新教材的背景下，新高考越来越重视对学科核心素养的考查.而解析几何部分涉及多种学科核心素养的特点也使其在高考中的地位愈发重要.解析几何的难点在于运算，而新高考的解析几何题目似乎已不再单纯是联立方程和韦达定理的固定模式那样简单，而是从根本上要求考生提高数学运算核心素养.新课标将数学运算核心素养总结为四大主要特
解题天地 | 倡导“一题多变”，实现“一题多得”

解题天地 | 倡导“一题多变”，实现“一题多得”

摘要：数学解题与研究一直是数学教学与学习过程中的一个重要研究课题，也是提升能力与开拓思维的基本场所.基于一道解三角形问题实例，合理分析与研究，从不同层面加以巧妙探究，合理变式拓展，实现问题的“一题多变”，达到问题的“一题多得”，引领并指导数学教学与解题研究. 关键词：三角形；面积；一题多变；变式；拓展借助一些典型的数学例（习）题，特别是高考真题、模拟题、自主招生题等，充分挖掘问题的已知条件与
解题天地 | 相邻三项线性递推关系数列通项的简便求法

解题天地 | 相邻三项线性递推关系数列通项的简便求法

摘要：熟练掌握数列通项公式的求解是高考以及各类考试的基本要求.在高中阶段，相邻三项线性递推关系数列通项公式的求解是一个难点，需要构造相邻两项的差为特殊数列进行求解，具有一定的难度.本文中在常规解法的基础上，用特征方程法快速准确地求解通项公式，大大缩短了求解时间. 关键词：递推数列；特征方程；通项公式 1一个实例及解法例1已知数列{an}满足a1=1，a2=2，且an+1=2an+3an－1
教师发展 | 教师专业错位化发展的实践与研究

教师发展 | 教师专业错位化发展的实践与研究

摘要：文章结合学校教师专业发展过程中的实际情况，由学科组内优秀教师引领，通过四个学术共同体错位化发展，最终达到学科组全体教师的共同成长. 关键词：错位化发展；高效课堂；试题研究中心；论文撰写；信息技术 1教师专业错位化发展的问题提出 1.1宏观层面 2022年4月2日教育部等八部门印发的《新时代基础教育强师计划》中指出，高质量教师是高质量教育发展的中坚力量.为贯彻落实《中共中央国务院关于全
教师发展 | 完善中学数学教师继续教育的策略

教师发展 | 完善中学数学教师继续教育的策略

摘要：中学数学教师继续教育的开展是必要的，它能够帮助中学数学教师丰富知识储备，提高各项教学技能，适应教育的不断变革.当前，中学数学教师继续教育仍存在教师认知偏差、制度不够完善、课程结构单一等问题.本文中提出了“转变教师观念，增强教师继续教育意识；健全政策制度，加强教师继续教育保障；形成多样教育，丰富教师继续教育形式”完善中学数学教师继续教育的几点策略. 关键词：中学；数学教师；继续教育教师是
教师发展 | 以生为主教学相长

教师发展 | 以生为主教学相长

新课程教学倡导以生为主体，以师为主导，构建师生协同发展的课堂教学模式，为社会培养全面发展的有用人才.基于此，高中数学课堂应改变传统以师为主的教学模式，为学生创造一个和谐发展的探究环境，让师生、生生相互启迪、相互激励、相互唤醒，建立平等、民主、和谐的师生关系，促进教学相长[1].笔者结合以下两个教学片段谈谈如何通过有效互动，优化教学过程，提升教学质量和学习品质，实现教学相长. 1教学片断案例1
教师发展 | 情境创设中存在的问题分析及教学建议

教师发展 | 情境创设中存在的问题分析及教学建议

摘要：随着新课改的推进，情境创设已然成为教育者的看家本领.实践证明，有些教师在情境创设上仍存在一些观念或行为上的不足.本文中结合在情境创设中容易出现的“流于形式，缺乏探究性；喧宾夺主，毫无导向性；固步自封，丧失数学味”三个方面的问题，用具体实例进行分析，并提出相应的教学建议. 关键词：情境创设；形式；趣味性 “新课标”提出：在教学活动中，要让学生亲历“情境创设—模型建立—解释应用”的过程.由此
教师发展 | 逐层深入，让“深度学习”真正发生

教师发展 | 逐层深入，让“深度学习”真正发生

深度学习是指在教师的引导下，学生围绕具有一定挑战性的主题，积极参与，充分体验知识的发生发展过程，获得思维有效生长的学习过程.这也是学生深刻掌握核心知识，把握数学本质，形成良好思维品质和积极情感态度与价值观的过程.本文中以一道试题的教学为例，具体谈谈如何逐层深入，让“深度学习”真正发生. 1重基础，通概念，获得理解能力只有夯实基础，才能筑起高楼大厦.概念是数学的基础，是获得数学知识与技能的核心
教师发展 | 基于“理解”的“余弦定理”课堂教学实践

教师发展 | 基于“理解”的“余弦定理”课堂教学实践

摘要：指向理解的教学设计给学生以更多的探究机会，其不仅可以让学生自然地接受新知识、理解新知识，而且通过新知与旧知的相互补充和融合，有利于学生知识体系的建构和数学综合学力的提升.在实际教学中，教师要打破“照本宣科”的教学模式的束缚，引导学生经历探究新知识的全过程，让学生真正理解数学知识. 关键词：理解；探究；综合学力在数学学习中，若想灵活应用数学知识解决问题，首先就要理解它，只有理解了才能更深
教师发展 | 关注个体发展实现有效教学

教师发展 | 关注个体发展实现有效教学

摘要：好的教学应该是学生高度参与的，能够促进学生个体发展的.在课堂教学中，教师要多一些关心、多一些信任，多给学生一些话语权和思考权，以此提高学生参与课堂的积极性，让学生学会思考、学会合作、学会交流，进而让学生获得更好的发展，让课堂变得更加鲜活. 关键词：好的教学；个体发展；积极性课堂是学生的课堂，有学生参与的课堂才是有效的.在课堂教学中，教师要关注学生这样的鲜活个体，学会站在学生的视角审视问
教师发展 | 关注二轮复习提升综合素质

教师发展 | 关注二轮复习提升综合素质

高三数学复习大体可以分为三轮，第一轮，抓基础，重“三基”；第二轮，抓专题，重方法；第三轮，抓策略，重拓展.以第二轮复习为例，其总目标是在“三基”的基础上，借助专题练习建构更全面、更完善的知识体系，提升学生解决实际问题的能力，提升学生的自信心[1].要实现这一目标，首先，教师要引导学生关注知识的本质特征，对知识体系有全面、整体的把握，以此提升学生的知识迁移能力，提高解决综合性问题的能力；其次，在解题
教师发展 | 倡导“三要”，回避“三忌”

教师发展 | 倡导“三要”，回避“三忌”

二轮复习是基于一轮复习后的一个重要阶段，关键在于学生的能力提升与素养养成，进一步构建并完善数学学科的知识体系结构与网络，以及更加全面的解题技巧与方法等.因而，为了更加有效地进行高考数学二轮复习，必须做到合理侧重点、横联纵拓面、聚集能力点等，在复习过程中要倡导“三要“，回避“三忌”. 1倡导“凸显主体”，忌讳“面面俱到” 在实际复习备考过程中，高考数学二轮复习有时也不是单独存在的一个完整区间段，
教师发展 | 开展主题教学，提升复习品质

教师发展 | 开展主题教学，提升复习品质

主题式教学以“核心议题”为焦点，将教学理论和生活实践有机结合起来，引导学生关注知识间的内在联系，充分发挥学生的主体作用，提升学生的数学应用水平.主题的范围是比较广泛的，它可以是一章或跨几章的内容，也可以是某种能力或者某个素养，还可以是一些章节的重要概念，等等.教师作为课堂教学的组织者，要打破单一知识、单一章节的束缚，着眼于全局，结合教学实际合理设计主题，充分发挥主题式教学的优势，提升复习教学品质.
教师发展 | 基于“抽象素养”培养的课堂教学实践与思考

教师发展 | 基于“抽象素养”培养的课堂教学实践与思考

摘要：数学抽象是反映客观现实事物的本质与规律的基本方式，它对促进学生理性思维与学科精神的发展具有重要意义.在数学抽象的基础上培育抽象素养可有效拔高学生的思维，为发展核心素养夯实基础.文章中以“导数的定义”教学为例，分别从“创设情境，激趣启思”“引入实例，初步探索”“新知建构，深化理解”“练习训练，应用定义”“归纳总结，巩固提升”等方面展开教学实践与思考. 关键词：抽象；素养；导数抽象素养指学
教师发展 | 基于“问题链”的高中数学教学实践

教师发展 | 基于“问题链”的高中数学教学实践

摘要：“问题”是数学的心脏.在问题的指导下，学生可以形成强烈的学习兴趣，可以在问题的指导下，深入课堂，认真学习，积极参加各种探究活动.通过问题的引导能培养学生的数学思维、探究意识.以问题链的方式设计圆的标准方程，能使学生更好地理解其本质，达到更好的学习效果. 关键词：问题链；高中数学；圆的标准方程新课程改革强调学生的素质教育、核心素养的培养，强调学生才是教学的主体，注重学生“四基”“四能”以

借助思维导图将思维“可视化”，探寻解题轨迹
重数学文化涵泳为学科素养赋能
聚焦数学结构之美挖掘文化育人价值
用理性精神让数学与物理适度融合
新人教A版与北师大版高中数学教材对比
依托教材，返璞归真：立体几何中的截面问题
SOLO分类理论指导下的教、学、评一体化设计
MPCK视角下的“基本不等式”单元教学
利用GGB软件辅助高中数学新教材函数教学
高中数学主题教学设计应把握四个关键点
迈向深度学习，优化复习效益
创新思维，优化策略
基于“三新”背景，高考备考建议
“概率统计”的复习备考建议
基于深度学习渗透核心素养
课例：函数的奇偶性
思维导图在整体性教学中的应用实践
“生本”理念下精彩习题课堂的建构
借助高质量提问打造高品质课堂
与时俱进时代特色，关注经济科技生产
从一道2023年高考题谈二面角的求法
泰勒公式与高考试题
“三叉戟”模型在解析几何中的深度应用
重构学习单元，创新学习指导
高考数学“概率与统计”试题的特点及其教学启示
拾级而上重本质，开拓进取升素养
研读高考试卷的三个层次
数山探路悟法理学海驾舟求真知
例谈帕德逼近在导数中的应用
基于数学命题方式，实现问题价值提升
对一道解析几何试题的探究与拓展
一道三角最值题的破解与拓展探究
2022年新高考Ⅰ卷第12题函数性质的思考
不等式情境，函数性视角
多角度探究圆锥曲线中的定值问题
切点弦场景创设，定点与动点轨迹
强化“三思维”，破解三角形
例谈不等式恒成立求参数范围问题的解题策略
线性规划常见题型及解法例析
“参数方程”的高三数学第一轮专题复习课例
不平移齐次化方法在圆锥曲线问题中的应用
一道新高考解析几何题的多解探究
倡导“一题多变”，实现“一题多得”
相邻三项线性递推关系数列通项的简便求法
教师专业错位化发展的实践与研究
完善中学数学教师继续教育的策略
以生为主教学相长
情境创设中存在的问题分析及教学建议
逐层深入，让“深度学习”真正发生
基于“理解”的“余弦定理”课堂教学实践
关注个体发展实现有效教学
关注二轮复习提升综合素质
倡导“三要”，回避“三忌”
开展主题教学，提升复习品质
基于“抽象素养”培养的课堂教学实践与思考
基于“问题链”的高中数学教学实践

过往期刊

更多

中学数学·高中版
2024年11期
中学数学·高中版
2024年10期
中学数学·高中版
2024年09期
中学数学·高中版
2024年08期
中学数学·高中版
2024年07期
中学数学·高中版
2024年06期
中学数学·高中版
2024年05期
中学数学·高中版
2024年04期
中学数学·高中版
2024年03期
中学数学·高中版
2024年02期
中学数学·高中版
2024年01期

猜你喜欢

时代英语·高一
2024年08期
时代英语·初中
2024年06期
高中数理化
2024年21期
发明与创新·上旬刊
2024年11期
语文世界(中学版)
2024年11期
发明与创新·下旬刊
2024年11期
中学生数理化·高二数学
2024年11期
少男少女·小作家
2024年11期

Copyright © 2017 龙源数字传媒集团京ICP备060024号
Dragonsource.com Inc. All Rights Reserved
IP:3.144.45.187

苏州工业园区教育局电子阅览室

首页
全部分类
排行榜
客户端下载

登录
个人中心我的收藏退出登录
简体 / 繁体

苏州工业园区教育局电子阅览室

忘记密码新用户

新用户注册

已有账户

注册成功

修改电子邮件