全部分类/
中学教育/
高中数理化

高中数理化

2024年10期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

突破重难点 | 教材中的一个恒等式的证明及应用

突破重难点 | 教材中的一个恒等式的证明及应用

教材是教师和学生备战高考的重要资料，因为高考试题命制的一个原则是“源于教材，而高于教材”，所以高考命题者很注重开发教材、研究教材，挖掘教材知识的考查价值和功能，许多高考试题所涉及的思想方法都源于教材．因此，在高考复习备考期间，教师应与学生回归教材，充分挖掘教材的指导性功能．本文以人教A 版普通高中教科书数学必修第二册２２页练习第３题为例，从试题呈现、试题证明、试题的变形及其几何意义、极化恒等式的
突破重难点 | 例谈放缩法证明一类数列不等式的策略

突破重难点 | 例谈放缩法证明一类数列不等式的策略

也就是放缩法中所说的“度”，如果“度”把握不好，就不能得到要证明的不等式，这给学生解决此类问题带来极大的困惑．基于此，本文对该类型问题进行分类和总结，得到六种常见的数列求和放缩模型，让学生感到这类数列不等式也是有法可依、有章可循的．
突破重难点 | 一型多变探本质,一法多用提能力

突破重难点 | 一型多变探本质,一法多用提能力

对教材上的经典例题、习题以及高考题，采用一型多变、一法多用的方式进行教学，对培养学生思维的广阔性、深刻性、探索性、灵活性、独创性无疑是一种有效途径．本文以高考题为例，以教材的例题和习题为本，以期通过一型多变、一法多用的训练，拓宽和深化学生解题思路，提高学生分析问题、解决问题的能力，培养学生创新思维能力．裂项相消法一词并没有在各版本教材中专门列出，但常用于求解教材的例题、习题和高考题．裂项相消法
突破重难点 | 掌握函数单调性,巧解“疑难杂症”问题

突破重难点 | 掌握函数单调性,巧解“疑难杂症”问题

函数单调性在分析函数性质、不等式证明、最值等问题中具有重要的作用，也是求解某些问题的巧妙方法，因此，函数单调性在高考中是必考内容．本文聚焦函数单调性的概念、性质和应用，灵活求解“疑难杂症”问题．
突破重难点 | 整体思想在三角函数相关问题中的应用

突破重难点 | 整体思想在三角函数相关问题中的应用

整体思想是考虑数学问题时不仅着眼于它的局部特征，更要把注意力和着眼点放在问题的整体结构上，通过对其进行全面深刻的观察，发现问题的整体结构特征，善于用“集成”的眼光把某些式子或图形看成一个整体，把握它们之间的关联，进行有目的的构造与整合，从而使问题化难为易，化繁为简，提高解题效率．整体思想是一种重要的数学思想方法，这种思想有着非常重要的应用，往往可使许多按常规方法解答比较烦琐甚至不可解的问题便捷获
突破重难点 | 剖析“导数应用”的备考要点

突破重难点 | 剖析“导数应用”的备考要点

导数是研究初等函数性质问题的重要工具，是历年高考命题的必考点，大多以压轴题的形式出现，对学生推理论证、化归与转化、运算求解等能力具有较高要求．导数应用是学生复习时的难点，因此，笔者结合导数应用的本质，结合近年高考试题进行分析，提出几个备考要点，供考生参考．
突破重难点 | 导数中的基本问题

突破重难点 | 导数中的基本问题

曲线的切线问题是高考数学中的热点问题，大家对“在一点处”和“过一点处”的切线问题比较熟悉，最近几年，过一点切线的条数及两曲线的公切线等成为新的热点问题．曲线的切线问题除了考查考生对导数几何意义的理解，还涉及对函数与方程、化归与转化、构造等思想方法的考查．
突破重难点 | 探析核心素养考查,明确高考命题方向

突破重难点 | 探析核心素养考查,明确高考命题方向

在新高考、新课标和新教材的“三新”背景下，数学明确了六大核心素养，即数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，这六大核心素养是育人价值的集中体现，也是数学课程目标的集中体现．本文以数列为研究对象，通过对高考题、教材的例题和习题的分析，探究六大核心素养的考查情况，旨在明确高考命题方向．例２（２０２０年全国Ⅲ 卷理１７，节选）设数列{an}满足a１＝３，an＋１＝３an
突破重难点 | 聚焦新定义问题

突破重难点 | 聚焦新定义问题

新定义题经常以高等数学为背景，但它考查的重点不是高等数学知识，更不是高等数学知识的直接运用．新定义题主要考查的是考生的数学阅读能力、数学学习能力以及对数学符号的理解能力和表达能力．新定义问题主要涉及如下题型．１）新定义运算符号; ２）与集合有关的新定义问题; ３）与数论有关的问题，如高斯函数、二进制、同余等; ４）数列与集合综合的新定义问题; ５）与函数有关的新定义问题; ６）与组
突破重难点 | 推导二项分布期望与方差,偶得一类分布列期望公式

突破重难点 | 推导二项分布期望与方差,偶得一类分布列期望公式

二项分布的期望与方差公式从形式上可以看成两点分布的期望与方差的n 倍．本文利用两点分布快速推导得到二项分布的期望与方差，并揭示独立事件和的期望与方差的性质，进一步得到一类“闯关分布”问题的期望公式，然后通过实例说明得到的相关性质在解题中的应用．
突破重难点 | 阿波罗尼斯圆的性质及其在解三角形中的应用

突破重难点 | 阿波罗尼斯圆的性质及其在解三角形中的应用

阿波罗尼斯圆（以下简称阿氏圆）是基于一个动点与两定点的距离之比为定值的视角，对圆本质特征的刻画．阿氏圆及其性质在解三角形中有着广泛的应用．下面对其进行拓广探究与迁移应用，以期实现模块知识融合，优化知识结构，提高解决问题能力．
突破重难点 | 欧拉线

突破重难点 | 欧拉线

瑞士数学家欧拉１７６５年在其所著的«三角形的几何学»一书中提出：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心的距离的一半，此直线被称为三角形的欧拉线，该定理被称为欧拉线定理．在各地新高考模拟试卷中，涉及欧拉线的试题频频“闪亮登场”，它们构思精巧、韵味十足、魅力四射，是考查考生的学科素养和关键能力的极好素材．下面精选一些例题加以剖析，旨在探索题型规律，揭示解题方法（通
突破重难点 | 巧用共线定理　简化数学运算

突破重难点 | 巧用共线定理　简化数学运算

«普通高中数学课程标准（２０１７年版２０２０年修订）»明确指出，基本理念包括把握数学本质，启发思考，改进教学．教师要从学生最近发展区出发，设计有联系的学习情境，设计思维连贯的问题串，在联系、对比、变化、拓展问题中把握本质，理解本质．在解析几何中，我们常遇到由一个定点引出一条动直线交椭圆于不同两点的几何特征问题，学生正向思维是设出直线方程，将之与椭圆方程联立，运用根与系数的关系解决问题．事实上，这
方法与技巧 | 小题小做

方法与技巧 | 小题小做

高考中涉及的分段函数问题通常会有一个参数，它可能在某一段函数的解析式中，也可能在分段的范围中，还有可能出现在问题的条件中．从知识考查方面来看，分段函数的考查常与函数的性质以及方程问题结合，重点考查分类讨论、数形结合的思想方法．解决分段函数的相关问题，应依据函数的定义，注意函数本身的整体性，遵循分段处理的原则，充分利用图的直观性与数的精准性进行动态分析处理，与此同时要关注临界状态和趋势判断．本文探求
方法与技巧 | 基于新高考的数学压轴题备考策略

方法与技巧 | 基于新高考的数学压轴题备考策略

２０２４年１月１９日—２１日，教育部组织了九省联考，其中语文、外语和数学是由教育部统一命题．此次联考的数学试卷采用了新的结构，其中选择题、填空题和解答题各减少了一题，而且题目的顺序和分值都发生了变化．九省联考数学试题的压轴题（即第１９题）是以离散数学中的离散对数为背景，考查初等数学的相关内容．这道题属于新定义题，也是以高等数学为背景进行考查的试题．自九省联考之后，各地的高三期末考试都参照九省联考
方法与技巧 | 基于函数单调性定义引发的思考

方法与技巧 | 基于函数单调性定义引发的思考

函数单调性是刻画函数性态的重要工具，是高中数学中的一个重要知识，也是高考的重要考点．人教A版普通高中教科书数学必修第一册中给出的函数单调性的定义是这样的．
方法与技巧 | 例说导数综合题中的取点方法

方法与技巧 | 例说导数综合题中的取点方法

导数综合问题中经常会涉及取点，如为了证明某函数有零点，需要找到自变量x（x∈D ）的两个不同取值x１，x２使得f（x１）＜０，f（x２）＞０，从而由零点存在定理得出函数在区间D 上存在零点．再如在证明一个全称量词命题错误或存在量词命题正确时，也需要找到一个特定的点，使得结论得证．学生在解决相关问题时，最大的障碍是如何取到合适的点x１，x２．基于此，本文结合近年北京各区模拟题和高考题，梳理相关取点
方法与技巧 | 剖析分离参数法在高考导数压轴题中的应用

方法与技巧 | 剖析分离参数法在高考导数压轴题中的应用

«普通高中数学课程标准（２０１７年版２０２０年修订）»对高中毕业的数学学业水平考试、数学高考的命题提出以下建议．考查内容应围绕数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用，强调基础性、综合性;注重数学本质、通性通法，淡化解题技巧．在导数压轴题中，不等式恒成立求参数范围问题，是高考中的热点问题，备受命题者的青睐，分离参数法是解决此类问题的一把利器，是一种通法，本文以九道导数试题
方法与技巧 | 合理选择研究角度,破解新情境下的数列问题

方法与技巧 | 合理选择研究角度,破解新情境下的数列问题

近年来高考或模考中的新情境问题，对学生的阅读、分析、判断、决策能力要求很高，找到“关键条件”或“好路径”，以此打开解题的思路十分重要，本文以两道试题为例，展示如何合理选择研究路径，以期提升解决问题的能力．对于A，当a１＝３时，如图３所示，作x ＝３与f（x）的图像相交于点A１，过点A１作y 轴的垂线与y＝x 相交于点B１，过点B１作x 轴的垂线与f（x）相交于点A２，点A１与A２
方法与技巧 | 动中有静,静中有动

方法与技巧 | 动中有静,静中有动

在高中数学中三角函数有着很重要的地位，它是联系几何与代数的桥梁，不仅仅自身有着独特的性质———周期性，同时也与其他知识有着紧密联系，有很多问题都可以借助三角函数得以解决．例如，通过选取角为变量，利用三角函数解决最值问题．近些年的高考中对于三角函数与解三角形的考查严格按照«普通高中数学课程标准（２０１７年版２０２０年修订）»中的要求，注重基础知识的巩固与理解，重点提升学生的数学核心素养．尤其是函数y
方法与技巧 | 利用函数凹凸性求解高考压轴题

方法与技巧 | 利用函数凹凸性求解高考压轴题

本文从教材习题出发，给出函数凹凸性的定义，并从代数运算与几何直观的角度对函数凹凸性进行解释，利用函数凹凸性解释高考导数问题的背景，最后在近３年的高考试题中进行验证，总结出一类导数问题的解决思路与方法．
方法与技巧 | 探究导数应用中分类讨论的切入点

方法与技巧 | 探究导数应用中分类讨论的切入点

分类讨论思想是高中数学重要的思想方法，通过分类可将问题化整为零，各个击破．分类讨论思想在数学解题中有着广泛的应用，如何选择分类不能一概而论，要视具体问题具体分析．本文以导数与函数综合问题中如何寻找分类讨论的切入点为例，提出几点建议，供读者参考．
方法与技巧 | 极化恒等式应用举例

方法与技巧 | 极化恒等式应用举例

平面向量是高考数学考查的重要内容之一，而且近几年对平面向量的考查越来越灵活，题型多样，解法多变，让人捉摸不定，其中对平面向量数量积的考查显得尤为突出．涉及平面向量数量积的有关问题，运用极化恒等式求解有时能起到出奇制胜的效果．当遇到两个同起点且角度不定、模长不定的向量，要求它们的数量积时，可以考虑利用极化恒等式这一重要结论，这也体现了数形结合这一重要的数学思想在解题中的应用．
方法与技巧 | 一类含有四个未知量的函数问题的解决策略

方法与技巧 | 一类含有四个未知量的函数问题的解决策略

近年来，高考数学试卷经常出现带有多个未知量的函数导数压轴题，例如，２０１８年全国Ⅰ卷理科第２１题、２０２１年新高考Ⅰ卷第２２题等．这类问题往往使得学生措手不及，很多学生看到题目中出现多个未知量就产生了畏惧心理，不知道如何下手．本文结合具体实例归纳这类含有四个未知量（两个参数＋两个极值点或零点x１，x２）问题的解决方法，使得学生解决这类问题更加得心应手．
方法与技巧 | 一道解析几何试题的解法探究

方法与技巧 | 一道解析几何试题的解法探究

１问题展示
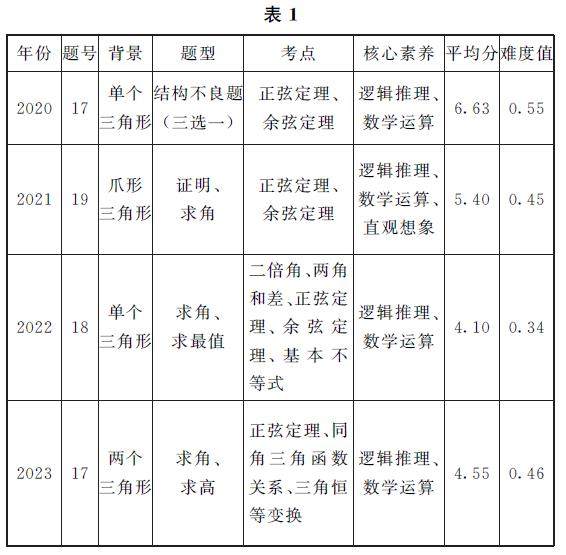
方法与技巧 | 谈谈２０２４年解三角形解答题备考策略

方法与技巧 | 谈谈２０２４年解三角形解答题备考策略

解三角形是每年高考的必考内容，主要考查必备知识和学科素养，题型稳定，难度适中，大多时候容易入手，但题型和图形结构需要联想到基础的解三角形模型，这对数学建模和逻辑推理素养提出了要求，考生容易出现会而不对、对而不全的情况．本文分析了近４年新高考Ⅰ卷解三角形解答题的特点，总结了解三角形必备的几个意识，并结合高考试题进行分析，提出了备考的建议，希望能对考生起到抛砖引玉的作用．１考点分析２０２０年
方法与技巧 | 一道九省联考解析几何大题的多解、探源与推广

方法与技巧 | 一道九省联考解析几何大题的多解、探源与推广

１试题呈现
方法与技巧 | 以光学原理为背景的解析几何多选题赏析

方法与技巧 | 以光学原理为背景的解析几何多选题赏析

在各地新高考模拟试卷中，以光学原理为背景的解析几何多项选择题频频“闪亮登场”，它们构思精巧、韵味十足、魅力四射，体现了新高考跨学科命题的理念，是考查学生的学科素养和关键能力的极好素材，具有很好的区分度和选拔功能．下面精选四类题型加以剖析，旨在探索题型规律，揭示解题方法．
方法与技巧 | 构造点线距离巧解一类最小值问题

方法与技巧 | 构造点线距离巧解一类最小值问题

近年来，与参数有关的最值问题在高考试题中反复出现，相关题型变化多样，通常考查分类讨论、转化与化归的数学思想，解法灵活，难度较大．若题目涉及两个或多个参数的最值问题，则难度会直线上升．本文着重介绍构造点线距离的方法解决一类“双参数”的最小值问题，供大家参考．
方法与技巧 | 立体几何动态问题的常见题型及求解策略

方法与技巧 | 立体几何动态问题的常见题型及求解策略

立体几何的动态问题是高考中具有创新意识的题型之一，它渗透了一些动态的点、线、面等元素，给静态的立体几何问题赋予了活力，使立体几何问题更具灵活性，突显了对学生空间想象能力的考查．常见题型有空间位置关系的判定、动点轨迹问题、最值（或范围）问题等．解决立体几何动态问题的关键在于要注重动态元素所引发的图形变化过程，动中窥静、静中见动、以静止动．下面归纳整理了立体几何中动态问题的常见题型及求解策略，希望对大
方法与技巧 | 概率统计:会看会算更会说

方法与技巧 | 概率统计:会看会算更会说

新课程标准实施后，高考数学学科加强了对概率与统计内容的考查．试题富有时代气息，基于生产、生活、科研等背景，展现“互联网＋”大数据时代特色．通过创设源于社会生活的真实情境问题考查学生的阅读、识图、计算、表达等能力，考查的核心素养是数据分析、数学运算．随着大数据时代的到来，概率与统计的重要性变得越来越突出．
方法与技巧 | 基于核心概念和几何意义问题的“破题”剖析

方法与技巧 | 基于核心概念和几何意义问题的“破题”剖析

概念是数学的起点，是数学思维的底层逻辑，而几何解释能更加直观地呈现概念的本质．解题过程就是对概念的运用和强化的过程，要求学生认真审题，找到“破题”技巧（参数的几何意义、设点坐标和极坐标应用就是三种不同类型的“破题”入口），在总结中重视四基，并且强化基本概念和几何意义，以助力高考数学备考复习．
强基计划 | 强基计划校考数学备考导引

强基计划 | 强基计划校考数学备考导引

笔者梳理自主招生与强基计划高校自主命题考试真题，得到１５个立意主题．高校自主命题的强基计划、综合评价以及清华大学自强计划、北京大学筑梦计划与中国科学技术大学少年班及创新试点班等各项招生数学命题都包含于这１５个主题．因此，备考强基计划校考应该从这１５个主题入手，要点梳理如表１所示，读者可参考本文备考应试．
强基计划 | ２０２４年北京大学强基计划校考数学备考策略

强基计划 | ２０２４年北京大学强基计划校考数学备考策略

北京大学强基计划（其前身是北京大学自主招生）于２０２０年正式实施，截至目前共实施了四年（２０２０—２０２３年），本文将阐述其试题特点并给出备考策略．
强基计划 | 探寻几何代数齐上阵,拓宽数量积最值求解

强基计划 | 探寻几何代数齐上阵,拓宽数量积最值求解

强基计划数学试题普遍具有很好的区分度，突出了数学基础学科的引领作用，着力考查学生的综合素养和创新意识，体现了为高校选拔优秀人才的目标．平面向量在高中数学学习中属于工具性的专题，有关平面向量数量积的最值问题是近几年各校强基计划校考中的热点问题．这类平面向量题目立足于向量的基本知识点，同时综合了数学中的其他知识点（如三角函数等），对于数学综合能力的考查比较到位，属于难题，向量数量积最值问题的求解有以
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(新高考Ⅰ卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(新高考Ⅰ卷)

（本试卷满分１５０分，考试用时１２０分钟）
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(新高考Ⅱ卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(新高考Ⅱ卷)

（本试卷满分１５０分，考试用时１２０分钟）
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国Ⅰ卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国Ⅰ卷)

（本试卷满分１５０分，考试用时１２０分钟）
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国Ⅱ卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国Ⅱ卷)

（本试卷满分１５０分，考试用时１２０分钟）
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国甲卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国甲卷)

（本试卷满分１５０分，考试用时１２０分钟）１８．如图所示，在四棱锥PＧABCD 中，PD ＝２AD ，PD ⊥DA ，PD ⊥DC，底面ABCD 为正方形，M ，N 分别为AD ，PD 的中点．（１）求证：PA ∥平面MNC; （２）求直线PB 与平面MNC 所成角的正弦值．１９．某村从事以紫长茄为主的蔬菜种植．受种植条件、管理水平、市场等因素影响，每年紫长茄的平均亩产量和统一收购价
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国乙卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(全国乙卷)

（本试卷满分１５０分，考试用时１２０分钟）１８．已知某科技公司的某型号芯片的各项指标经过全面检测后分为Ⅰ级和Ⅱ级，两种品级芯片的某项指标的频率分布直方图如图所示．若只利用该指标制定一个标准，需要确定临界值K ，按规定将该指标大于K 的产品应用于A 型手机，小于或等于K 的产品应用于B 型手机．若将Ⅰ级品中该指标小于或等于临界值K 的芯片错误应用于A 型手机会导致芯片生产商每部手机损失８００
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(北京卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(北京卷)

（本试卷满分１５０分，考试用时１２０分钟）
高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(天津卷)

高考模拟 | ２０２４年普通高等学校招生全国统一考试模拟试卷数学(天津卷)

（本试卷满分１５０分，考试用时１２０分钟）

过往期刊

更多

猜你喜欢

苏州工业园区教育局电子阅览室