目录
快速导航-
卷首语 | 找寻专属的教研“北极星”
卷首语 | 找寻专属的教研“北极星”
-

专题研究 | “分数”意义知多少
专题研究 | “分数”意义知多少
-
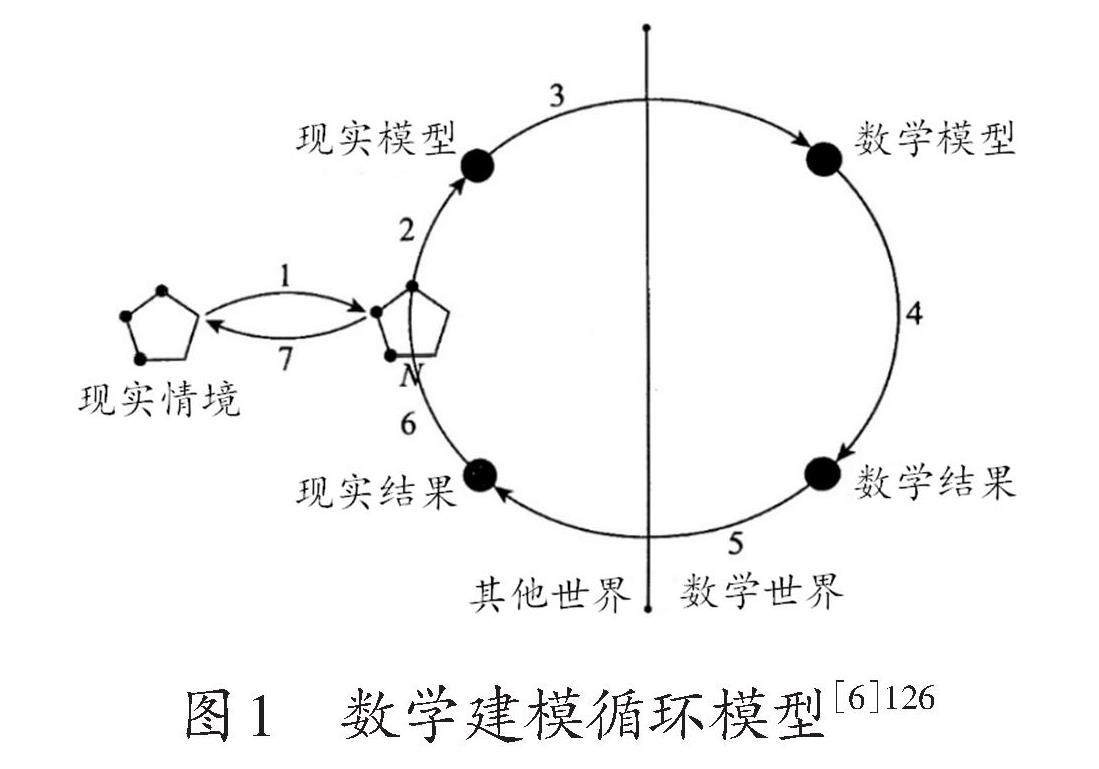
本期话题 | 数学建模力:内涵、价值与测评工具设计
本期话题 | 数学建模力:内涵、价值与测评工具设计
-
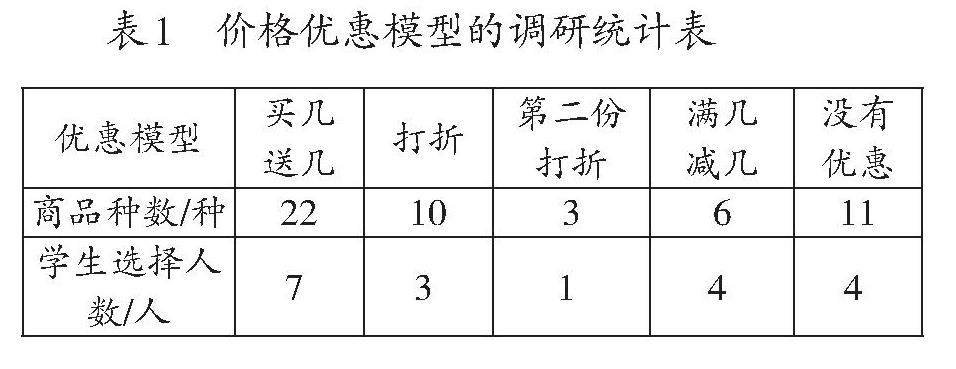
本期话题 | 经历建模过程 形成模型结构
本期话题 | 经历建模过程 形成模型结构
-

本期话题 | 经历情境数学化 感悟建模一般化
本期话题 | 经历情境数学化 感悟建模一般化
-
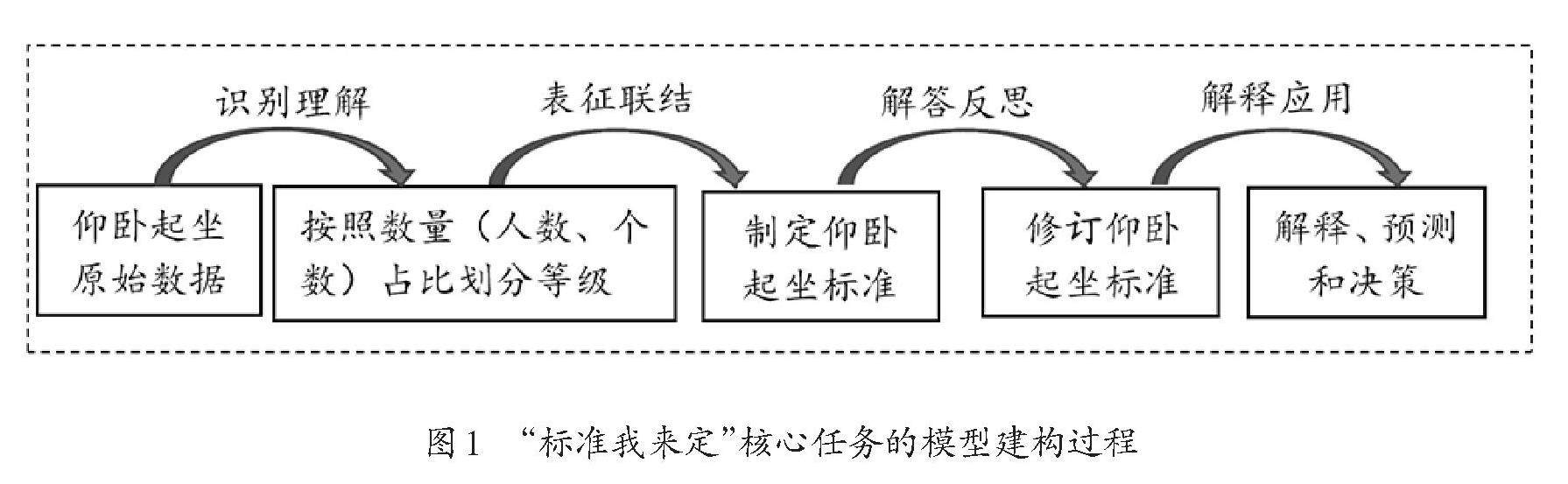
本期话题 | 指向建模力提升的核心任务设计与实践
本期话题 | 指向建模力提升的核心任务设计与实践
-

本期话题 | 数学化表征·一般化模型·迁移性应用
本期话题 | 数学化表征·一般化模型·迁移性应用
-

特别关注 | 基于学习路径的“分数加减法”单元整体教学
特别关注 | 基于学习路径的“分数加减法”单元整体教学
-

备课之窗 | 在关联与思辨中感悟运算的一致性
备课之窗 | 在关联与思辨中感悟运算的一致性
-

备课之窗 | 如何更好地认识比100大的数
备课之窗 | 如何更好地认识比100大的数
-

备课之窗 | 如何借助分数墙深入理解分数的意义
备课之窗 | 如何借助分数墙深入理解分数的意义
-
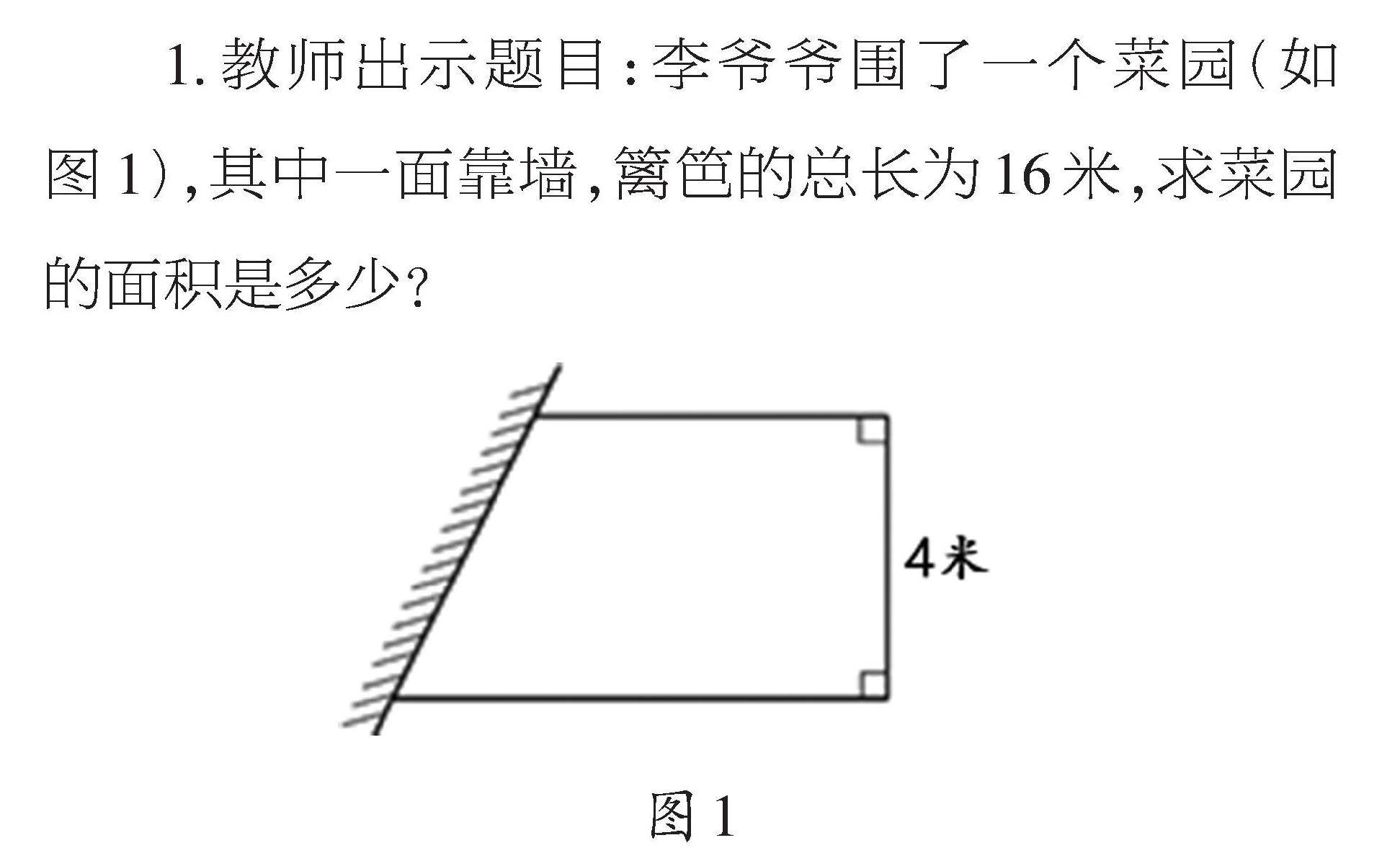
备课之窗 | 如何运用“整体思想”巧解数学问题
备课之窗 | 如何运用“整体思想”巧解数学问题
-
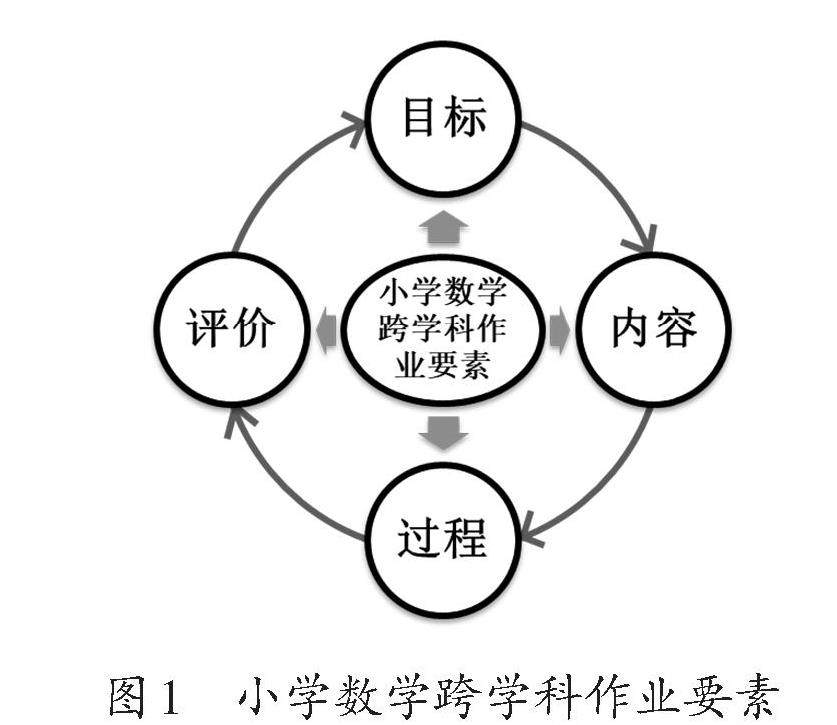
课堂新探 | 小学数学跨学科作业设计要素与策略
课堂新探 | 小学数学跨学科作业设计要素与策略
-

课堂新探 | “三案”导学:指向金融素养,促进深度学习
课堂新探 | “三案”导学:指向金融素养,促进深度学习
-
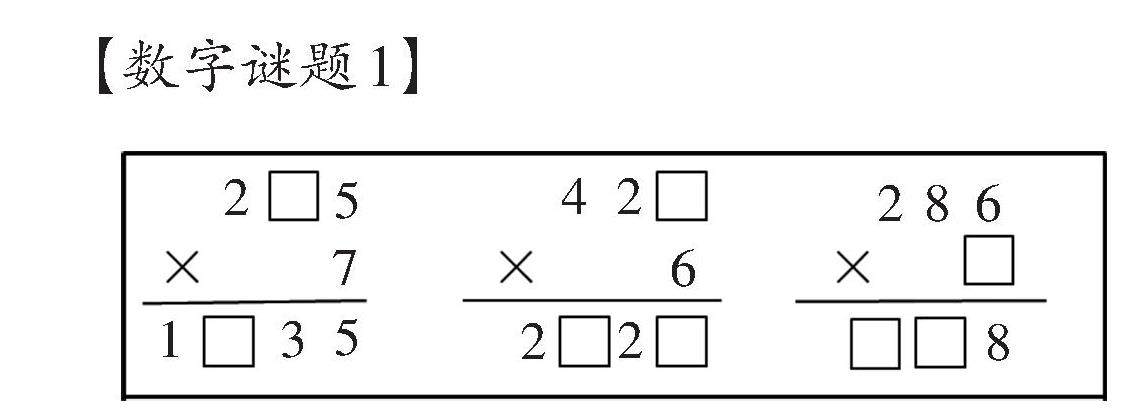
课堂新探 | 探寻·构建·生长
课堂新探 | 探寻·构建·生长
-
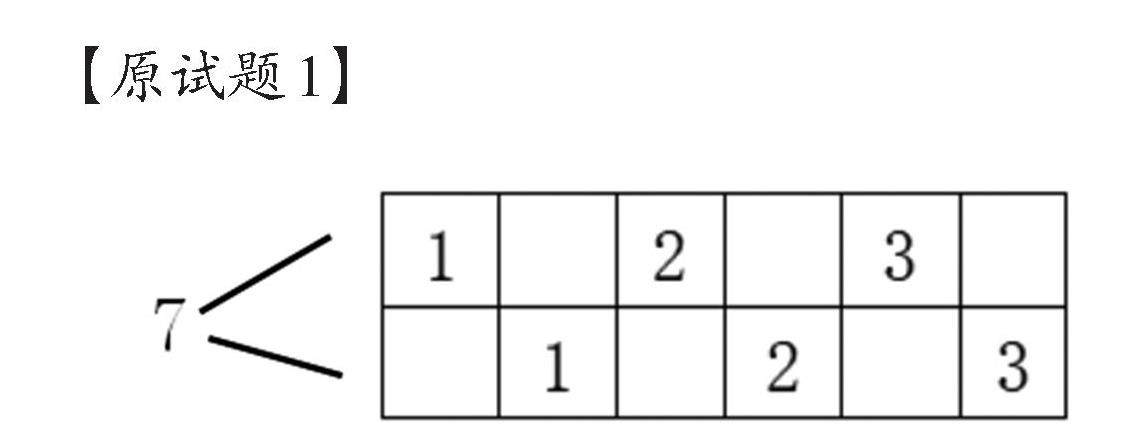
评价研究 | 真实情境在数学命题中的价值意蕴及设计策略
评价研究 | 真实情境在数学命题中的价值意蕴及设计策略
-
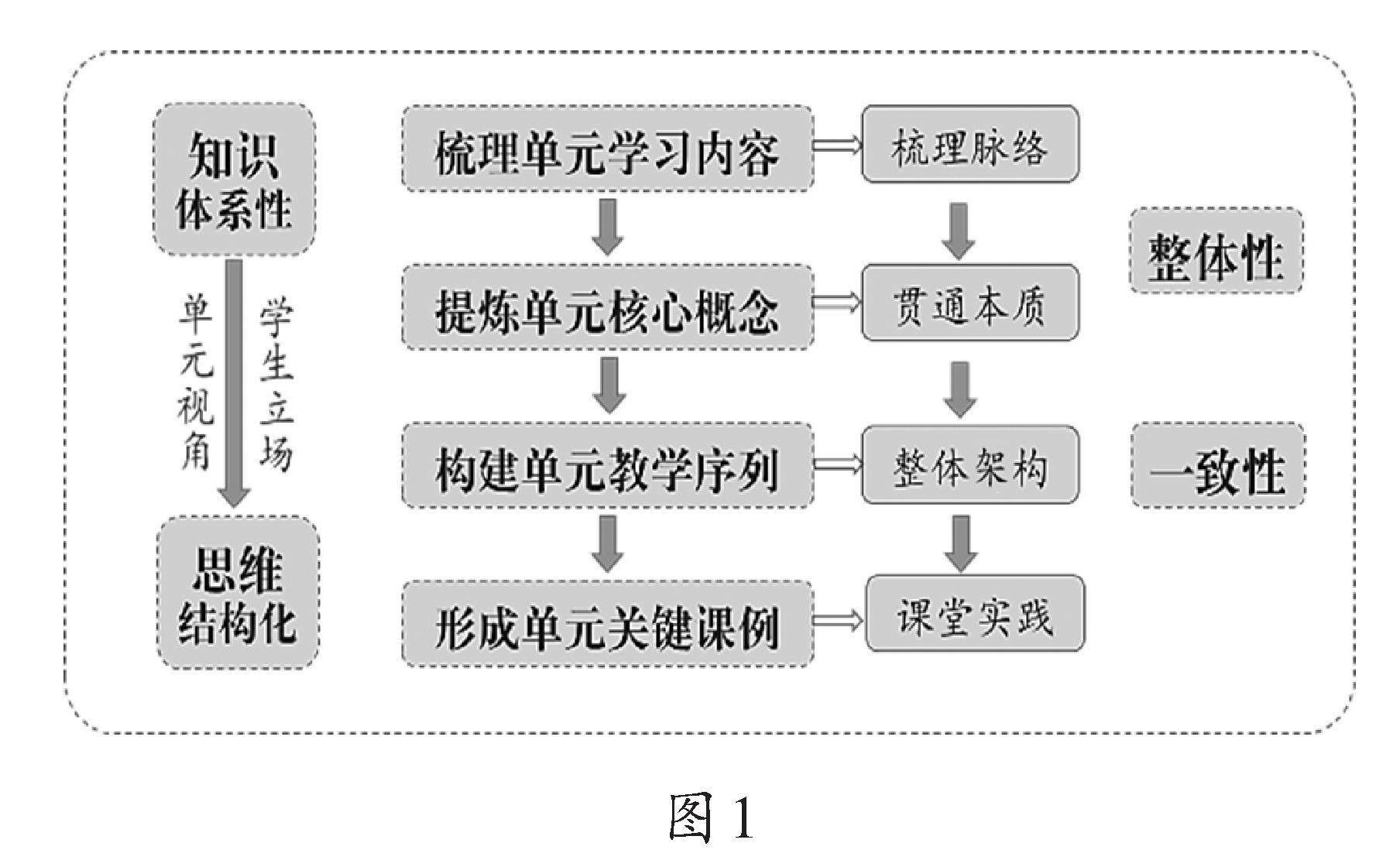
教师发展 | 素养立意,探寻有效的数学教学
教师发展 | 素养立意,探寻有效的数学教学




















 登录
登录