全部分类/
中学教育/
中学数学·初中版

中学数学·初中版

2024年02期

扫码免费借阅

目录

快速导航

特色展台 | 基于“后建构”课堂模型的结构化教学实践

特色展台 | 基于“后建构”课堂模型的结构化教学实践

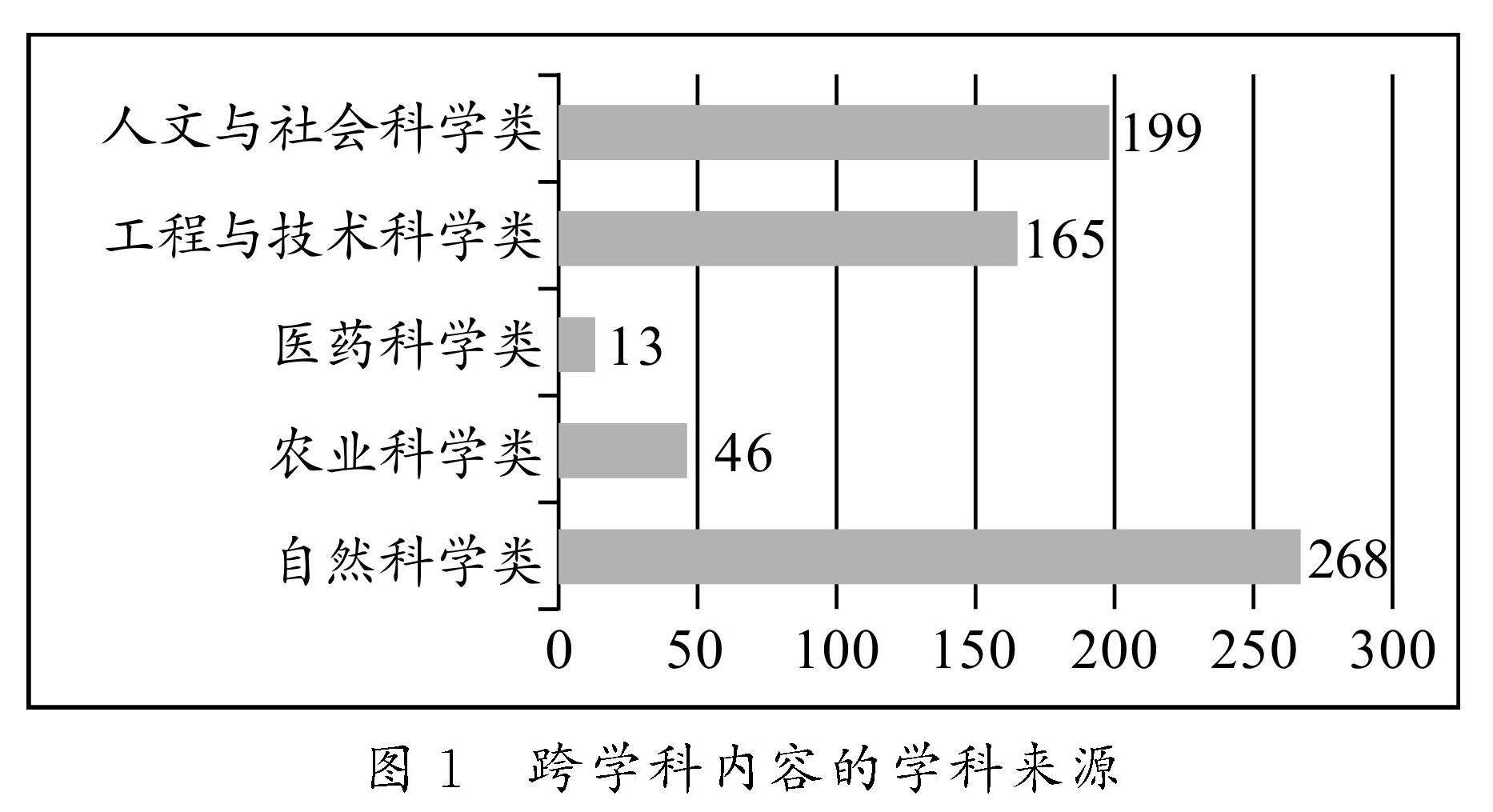
课题信息：江苏省中小学教学研究第十三期重点资助课题“指向学科核心素养的数学‘后建构’课堂设计研究”，课题编号为2019JK13.ZB16;江苏省教育科学“十四五”规划课题“基于学生认知发展的初中数学结构化教学实践研究”，立项编号为D/2021/02/688． 1 问题的提出 “一次函数、一元一次方程和一元一次不等式”是苏科版八年级上册6.6节的内容，首次将数学中最重要的函数模型、方程模型与不等
课程视点 | 数学教材跨学科内容分析

课程视点 | 数学教材跨学科内容分析

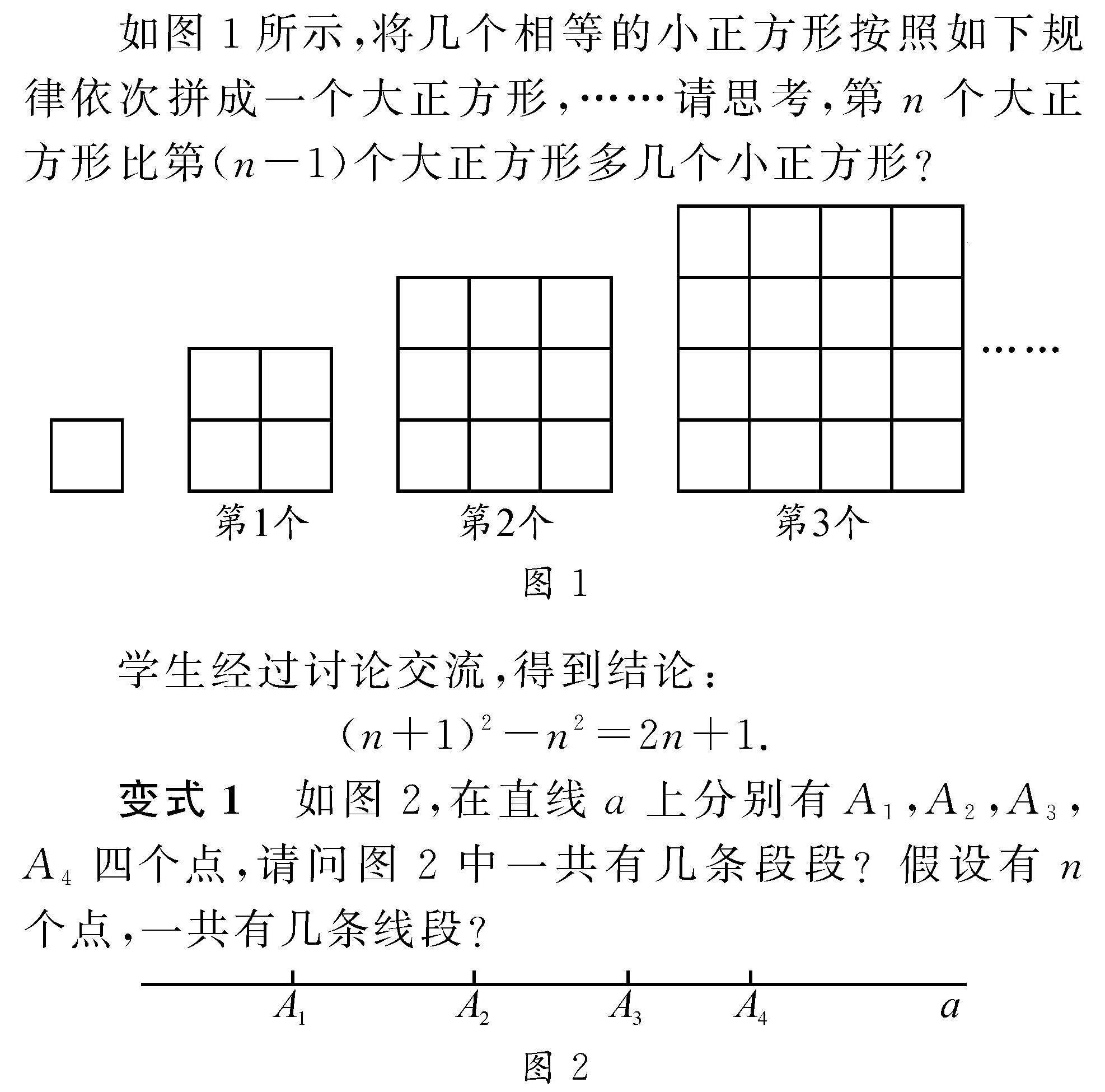
摘要：基于跨学科视角，从学科来源、呈现位置、使用目的三个维度，统计分析教材中跨学科内容特征.发现教材中跨学科内容涉及的学科类别多，但比例不协调.针对问题，得到启示，即适当调整素材分布，拓展跨学科融合深度，调整某一版块涉及的跨学科内容太单一的现象. 关键词：初中；数学教材；跨学科 1 引言近年来，跨学科教育理念受到大家广泛的关注.与传统教育理念相比，跨学科教育打破了不同学科的界限，重视学科间
课程视点 | 教材例题巧应用，思维能力促提升

课程视点 | 教材例题巧应用，思维能力促提升

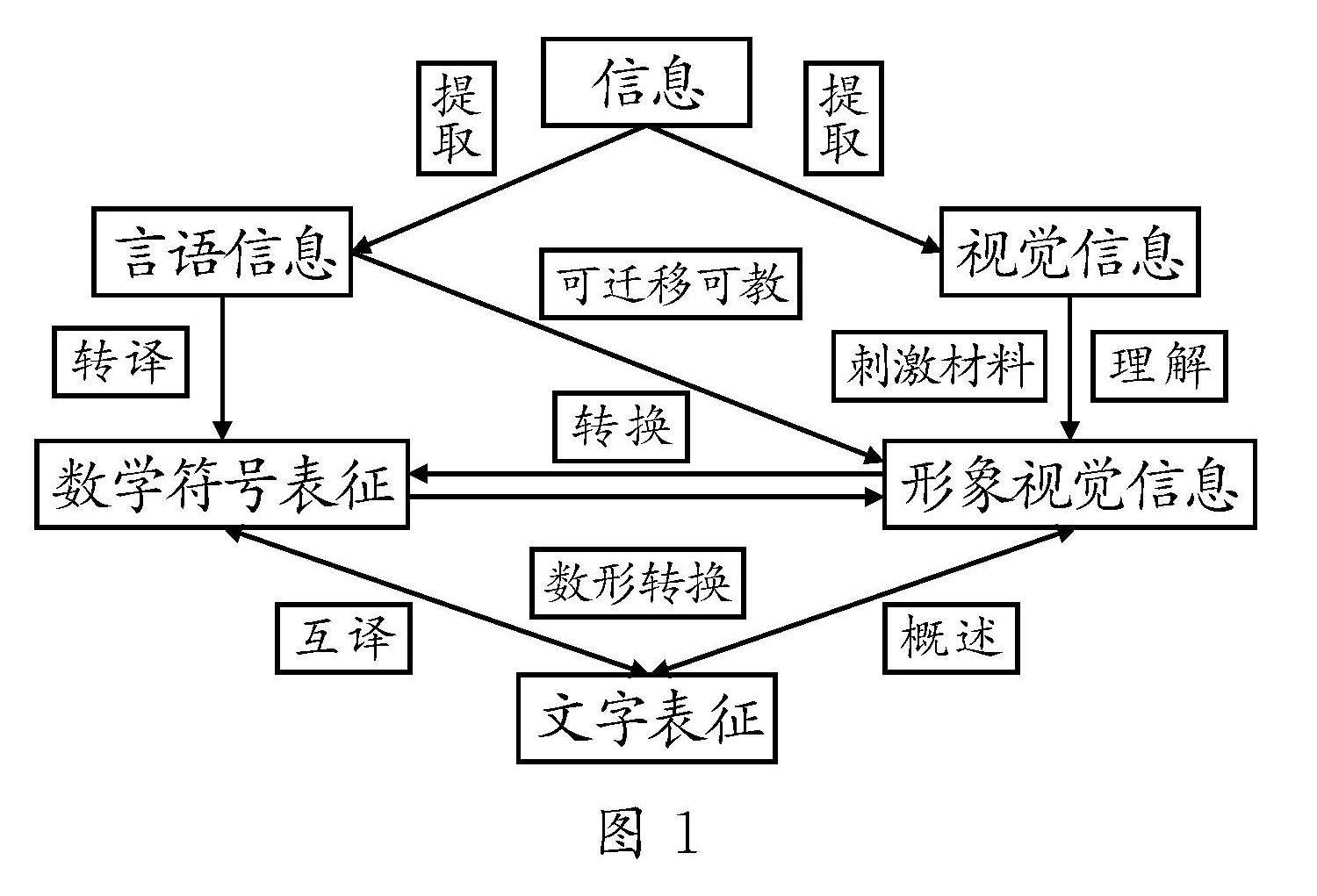
摘要：教材例题是编写人员围绕教学内容精心筛选的经典试题，目标明确，内涵丰富，是教学的重要素材，也是学生学习的重要载体.教师要充分挖掘教材例题的潜在功能，丰富例题内容，拓展例题内涵，使学生从一道例题的探究中掌握一类题的解法，强化理解数学知识，掌握数学思想和方法，提升知识迁移的能力，实现高效学习. 关键词：教材例题；数学思想；高效学习教材是教师教学和学生学习的重要资源.因此，要上好一节课，教师首
教法探索 | 基于视觉化表征的初中代数教学策略研究

教法探索 | 基于视觉化表征的初中代数教学策略研究

课题信息：广州市教育科学规划2022年度课题“基于视觉化表征的初中数与代数教学的实践研究”，课题编号为202214187. 初中数与代数的学习是符号的学习，而代数思维是一种形式的符号操作，代数知识可用可视的（图表、图象或曲线图）、数字的（表格、清单）、符号、口语呈现.灌输式的讲授方式，由于不能合理使用多媒体及缺少视觉化表征理论，不能起到减负增效的作用.本文中基于非线性结构主干理论、认知负荷、多元
教法探索 | 培养初中生函数与方程思想的策略研究

教法探索 | 培养初中生函数与方程思想的策略研究

课题信息：江苏省教育科学“十四五”规划2021年度重点课题“初中数学‘理趣相融深度互动’课堂学习策略研究”，课题总序号为B/2021/02/203. 摘要：为了更好地渗透函数与方程思想，教师应认真研究教材，充分挖掘教材中和函数与方程相关的教学内容，通过有目的、有意识的启发，指导学生自主发现二者的内在联系，理解函数与方程思想的本质，结合应用与反思让学生在深刻理解、掌握函数与方程思想的基础上，将其内
教法探索 | “微课”不“微”：谈微课在中学数学课堂中的应用

教法探索 | “微课”不“微”：谈微课在中学数学课堂中的应用

摘要：微课作为一种辅助教学方式，以其短小精悍且利用率高等特点演绎出一种新的课堂模式.微课一般以简短视频为主要载体，围绕学习过程中某个知识点，呈现出一定的逻辑组织关系，建构了一个半结构化、主题式的资源单元应用“小环境”.微课能激发学生的兴趣，打破课堂教学的时空局限，帮助理解知识的抽象生涩，实现课堂教学的课外延伸.微课的出现，提升着课堂的授课质量，推动着教学目标的实现. 关键词：微课;应用;激发兴趣
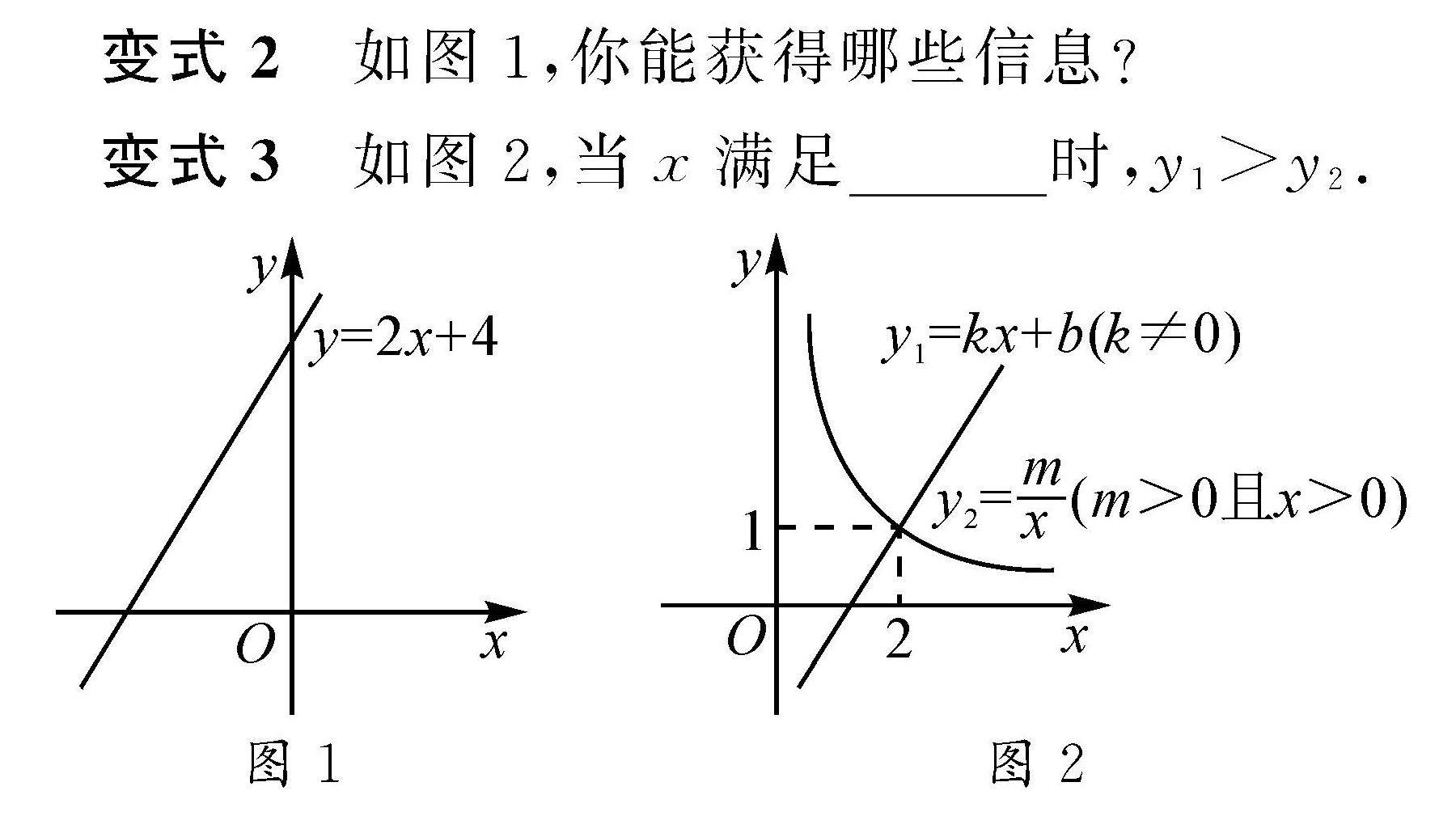
教法探索 | 初中数学教学中的变式教学

教法探索 | 初中数学教学中的变式教学

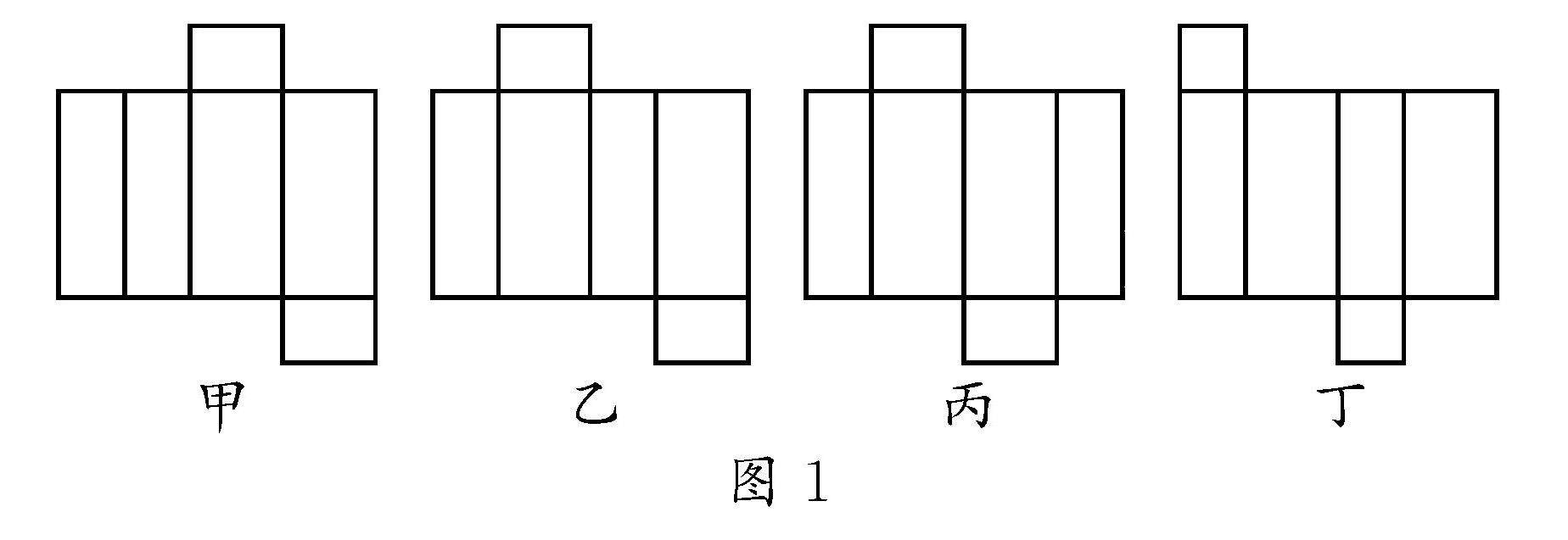
摘要：在初中数学教学中，变式教学是一个重要的环节.通过变式教学，可以帮助学生提高对知识的理解与认识，促进思维的深度发展，增强解决问题的能力.因此，教师需要重视变式教学，不断提升变式教学水平.本文中主要探讨了初中数学变式教学的常用方法，给出了对变式教学的几点思考. 关键词：变式教学；初中；数学教学变式作为初中数学中的重要内容之一，是学生学习数学的关键之一.在初中数学教学中，如何有效开展变式教学
教法探索 | 引导思考，启发教学：多角度拓展数学思维能力

教法探索 | 引导思考，启发教学：多角度拓展数学思维能力

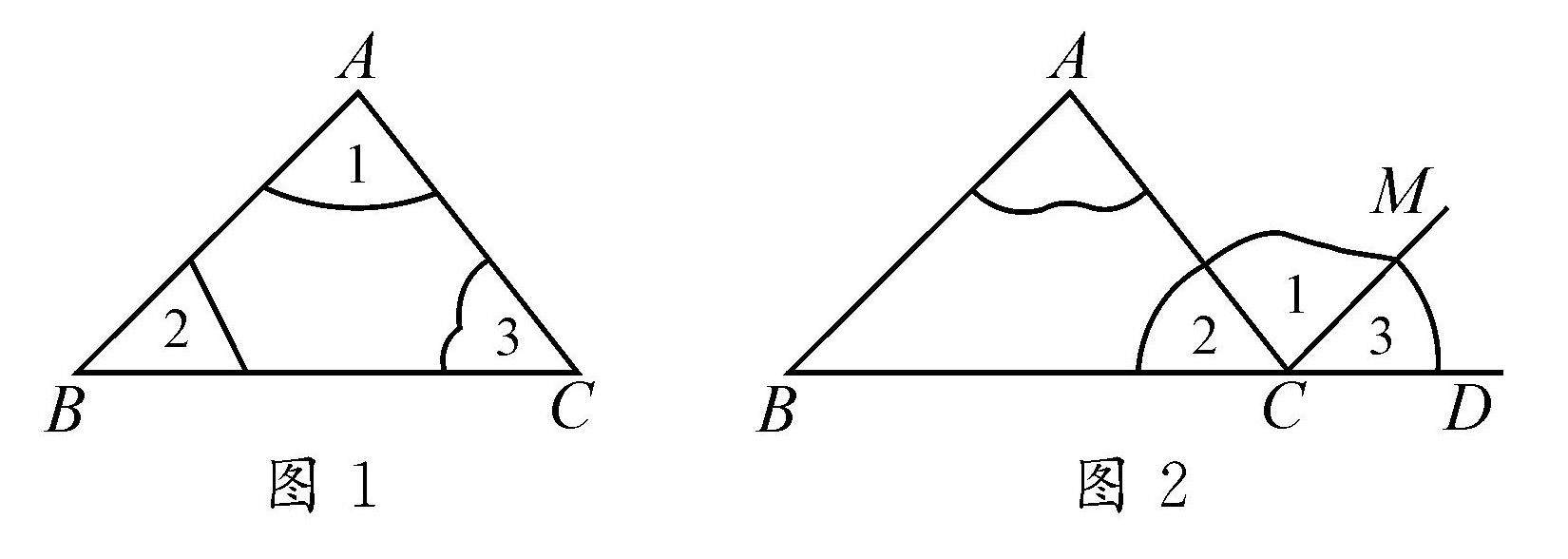
摘要：初中数学课堂启发式教学的出发点是根据学生认识的客观规律以及学生的学科思维能力和学情，充分驱动他们学习的主观能动性，激发探究知识奥秘的兴趣.启发式教学的基本点在于在教学中通过引导学生参与学习过程，经过自主思考和交流，将数学知识内化为学科素养，从而提高存疑、探疑和释疑的能力.可以说，启发式教学涵盖了当下教学思想和教学方法的总特征. 关键词：启发式;数学思维;能力实践证明，启发式教学法具有激
教法探索 | 例谈初中数学课堂教学中的情境创设

教法探索 | 例谈初中数学课堂教学中的情境创设

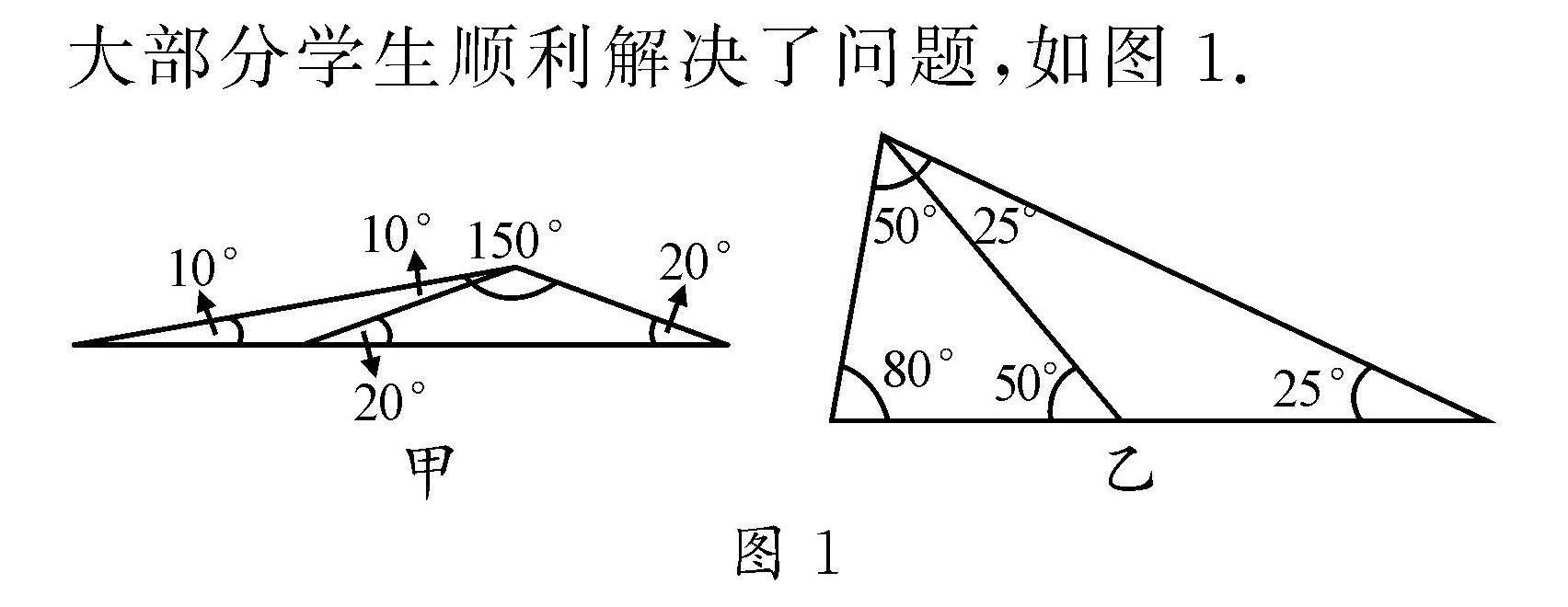
摘要：创设教学情境是引导学生在情境中主动探索学习、获取知识、体会数学思想的教学方法.教学情境的创设能够激发学生的学习兴趣，有效落实学生的主体地位，培养学生的探究精神.本文中从创设情境引入、探究和总结三个方面探讨创设情境的具体方法. 关键词：情境创设；课堂教学；学生主体情境创设是指教师围绕教学内容，有目的地创设问题情境的策略.通过情境的创设营造强烈的课堂求知气氛，进而激发学生的求知欲，促使学生
教法探索 | 搭建探究平台促进思维深耕

教法探索 | 搭建探究平台促进思维深耕

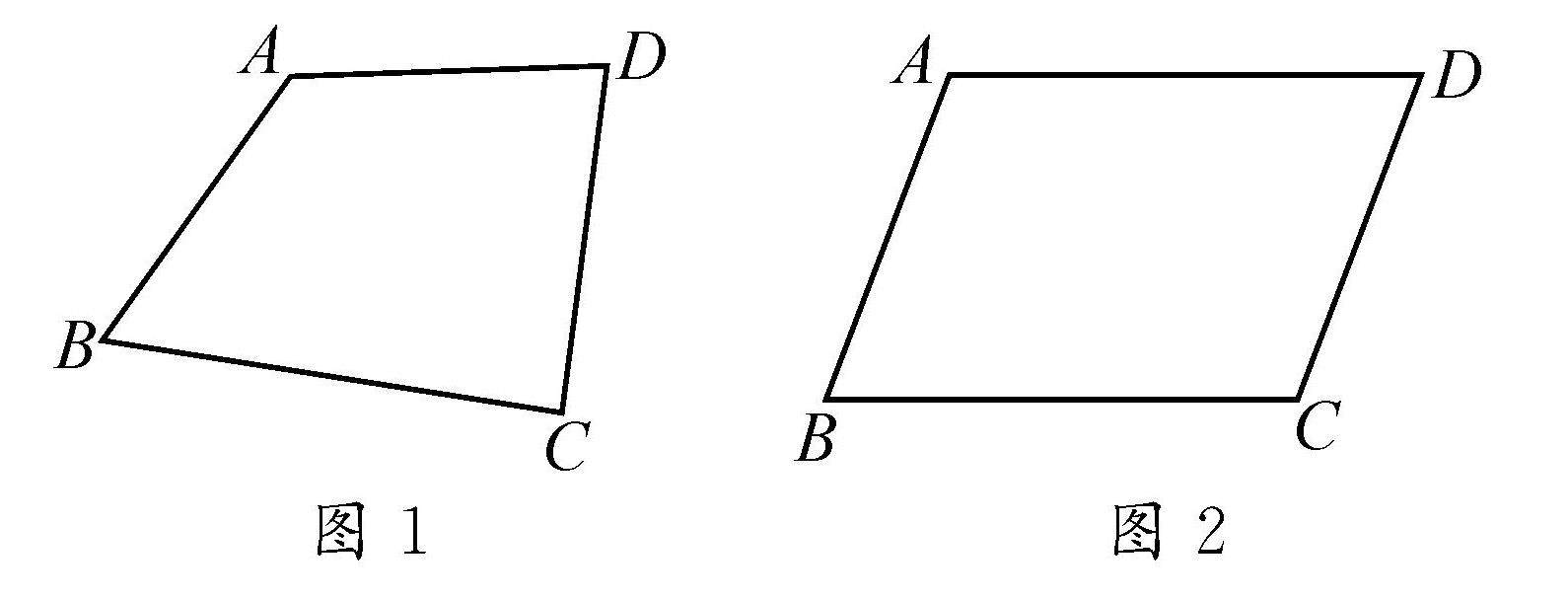
《义务教育数学课程标准（2022年版）》指出：要选择能引发学生思考的教学方式，改变单一讲授式教学方式，注重启发式、探究式、参与式、互动式教学，让学生在实践、探究、体验、反思、合作、交流等学习过程中感悟基本思想，积累基本活动经验，促进核心素养的发展.数学探究活动就是在表达、质疑、探究、讨论、理解等一系列过程中形成的一种主动探求知识以及重视解决问题的学习方式，是培养学生实践能力和创新精神的有效手段，可
教法探索 | 新授课情境创设：简明并有利新知生成

教法探索 | 新授课情境创设：简明并有利新知生成

摘要：新知引入阶段的情境创设是每节新授课的备课重点.然而有些情境创设由于故弄玄虚、人为编造、过多关联，导致新知引入环节过于冗长，反而不利于新课引入.一般来说，新知生成阶段最好能简洁明了、开门见山，有利于学生“去情境化”，自主概括数学概念，理解数学本质. 关键词：情境创设；公开课；平行四边形；新知导入 1 从一节“平行四边形的性质”教学引入说起在一次规模较大的教研会的名师课堂教学展示活动中，
教法探索 | 渗透数学思想彰显核心素养

教法探索 | 渗透数学思想彰显核心素养

摘要：数学核心素养是数学课程目标的集中体现.本文中以“二次函数与一元二次方程”的教学设计为例，说明在数学课堂中注重数学思想渗透的重要性，利用类比、转化、数形结合等数学思想，让复杂问题简单化、抽象问题具体化，有助于学生把握数学本质，培养理性思维，发展数学核心素养. 关键词：教学设计；数学思想；核心素养教育部颁布的《义务教育数学课程标准（2022年版）》明确指出：数学课程设计要体现数学学科特征，
教法探索 | 创新意识导向的初中数学教学

教法探索 | 创新意识导向的初中数学教学

摘要：透过课程标准的解读，厘清创新意识的内涵，从整体方位着手，并结合“反比例函数的图象与性质（第一课时）”的部分教学片断，提出在常态课中培养创新意识的策略.其中，好的问题引领是激发创新意识的前提，好的教学观念是培养创新意识的关键. 关键词：创新意识；数学教学；反比例函数《义务教育数学课程标准（2022年版）》倡导“应从义务教育阶段做起，落实创新意识的培养，并贯穿数学教育的始终”，在培养学生的
教法探索 | 巧设问题，点燃思维活力

教法探索 | 巧设问题，点燃思维活力

新课程改革的推进逐渐改变了课堂教学的模式、内容和方法，新的教学理念要求教师转变传统观念，成为课堂教学的引导者和组织者，落实学生的主体地位.教师在教学中要鼓励学生主动参与学习活动，在实践操作、合作探究、师生交流中获得知识和技能的提升.而课堂问题是联系师生思维活动的纽带，是点燃学生思维活力的钥匙.巧妙的问题设计能够加强师生之间的有效沟通交流，促进学生思维的发展，驱动学生有效完成自主探究活动，使教学活动
教法探索 | 例谈创设数学问题情境的路径

教法探索 | 例谈创设数学问题情境的路径

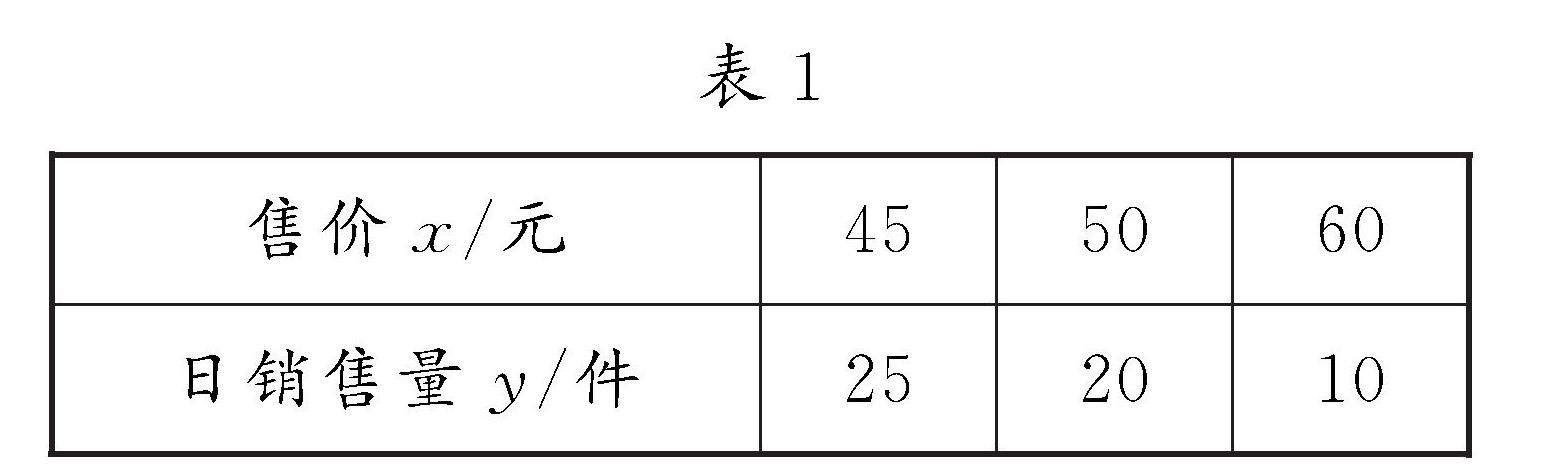
摘要：问题情境的设置是根据学生的已有知识经验，联系实际生活，在具体问题中融入数学知识的一种教学策略.创设问题情境使学生能够主动发现问题、分析问题和思考问题，调动学生的高阶思维活动，促进深度学习.本文中从结合数学史实、联系现实生活、进行操作实验、拓展变式训练四个方面讲述数学问题情境的创设，发展学生的思维品质，落实核心素养的目标. 关键词：问题情境;生活实际;学习兴趣;思维品质创设问题情境是数学
教法探索 | 问题驱动深度参与落实素养

教法探索 | 问题驱动深度参与落实素养

近日，笔者在参加全市乡村共同体数学教研活动中，听了一节乡镇学校的初三数学课，课题是“二次函数的应用”.课后，笔者进行了师生访谈交流，并对学生进行了检测分析，交流结果与分析数据引发了笔者对本节课一个教学片段的思考. 1 教学实录片段教者出示题目：某公司销售一批产品，该产品每件成本是40元，试销阶段每件产品的销售价x（单位：元）与产品的日销售量y（单位：件）之间满足一次函数关系，部分对应数据如表
教法探索 | “双减”背景下打造农村初中数学高效课堂

教法探索 | “双减”背景下打造农村初中数学高效课堂

摘要：在“双减”背景下，教师要切实减轻学生的课业负担，促进他们身心的健康发展.教学中要打造高效课堂，提升课堂教学质量，让学生的思维、能力、素养等在课内获得充足的发展.对农村初中的教学来说，教师要构建高效课堂，就必须结合学生学习的实际情况，发现并纠正当前教学中存在的问题，探究和创新教学方式，进而提升学生的综合素养. 关键词：初中数学；“双减”背景；高效课堂数学课堂教学本质上是学生与教师有效配合
学生学习 | 非智力因素视角下培养数学问题提出能力的实验研究

学生学习 | 非智力因素视角下培养数学问题提出能力的实验研究

项目信息：江汉大学教研项目“数学学科教学法案例库教学与案例库建设”，项目编号为2021X013，吴秀君为通讯作者. 摘要：问题提出是学生需要掌握的一项重要能力，培养和提高学生的数学问题提出能力具有重要意义.本文中基于智力与非智力因素的结合论、学习动机理论及“情境—问题”教学模式，对武汉市某中学七年级学生进行了一个学期的教学实验研究.得出，实验班学生在非智力因素水平及数学问题提出能力上全面优于对照
学生学习 | 加强多元表征策略研究，提升几何直观核心素养

学生学习 | 加强多元表征策略研究，提升几何直观核心素养

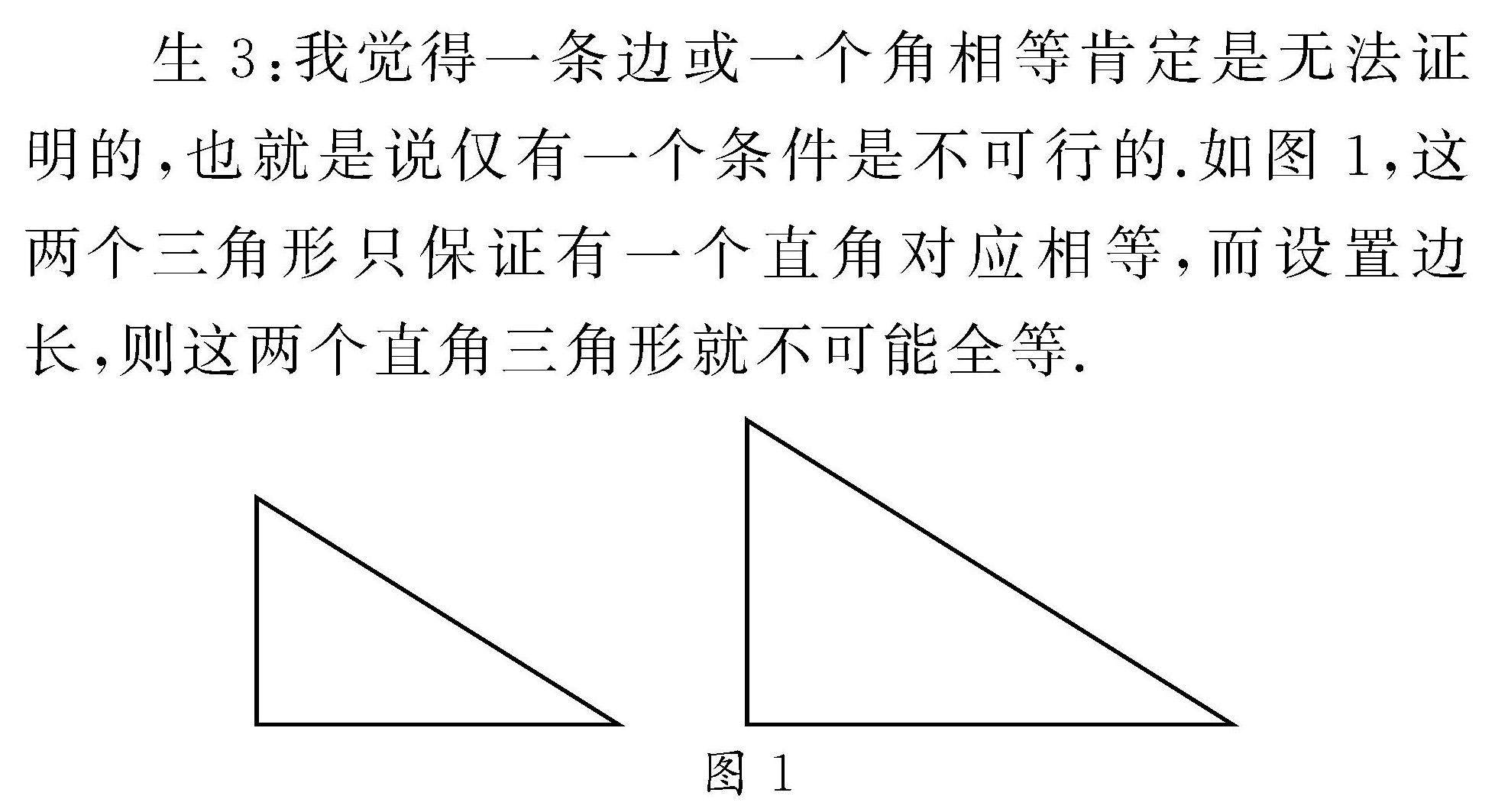
摘要：基于“如何充分利用多元表征策略，不断提升学生几何直观核心素养”的研究分析，主要从丰富语言情境表征、加强动态展示表征、强化数形结合表征、开展实践操作表征、构建数学模型表征五个方面，充分体现学生几何直观的“五度”. 关键词：初中数学；多元表征；几何直观；核心素养；策略研究在初中阶段数学知识的学习过程中，充分利用多元表征理论进行学生几何直观能力培养，可以多方面引导学生对数学问题的理解与研究，
学生学习 | 基于数学关键能力培养的探究性学习

学生学习 | 基于数学关键能力培养的探究性学习

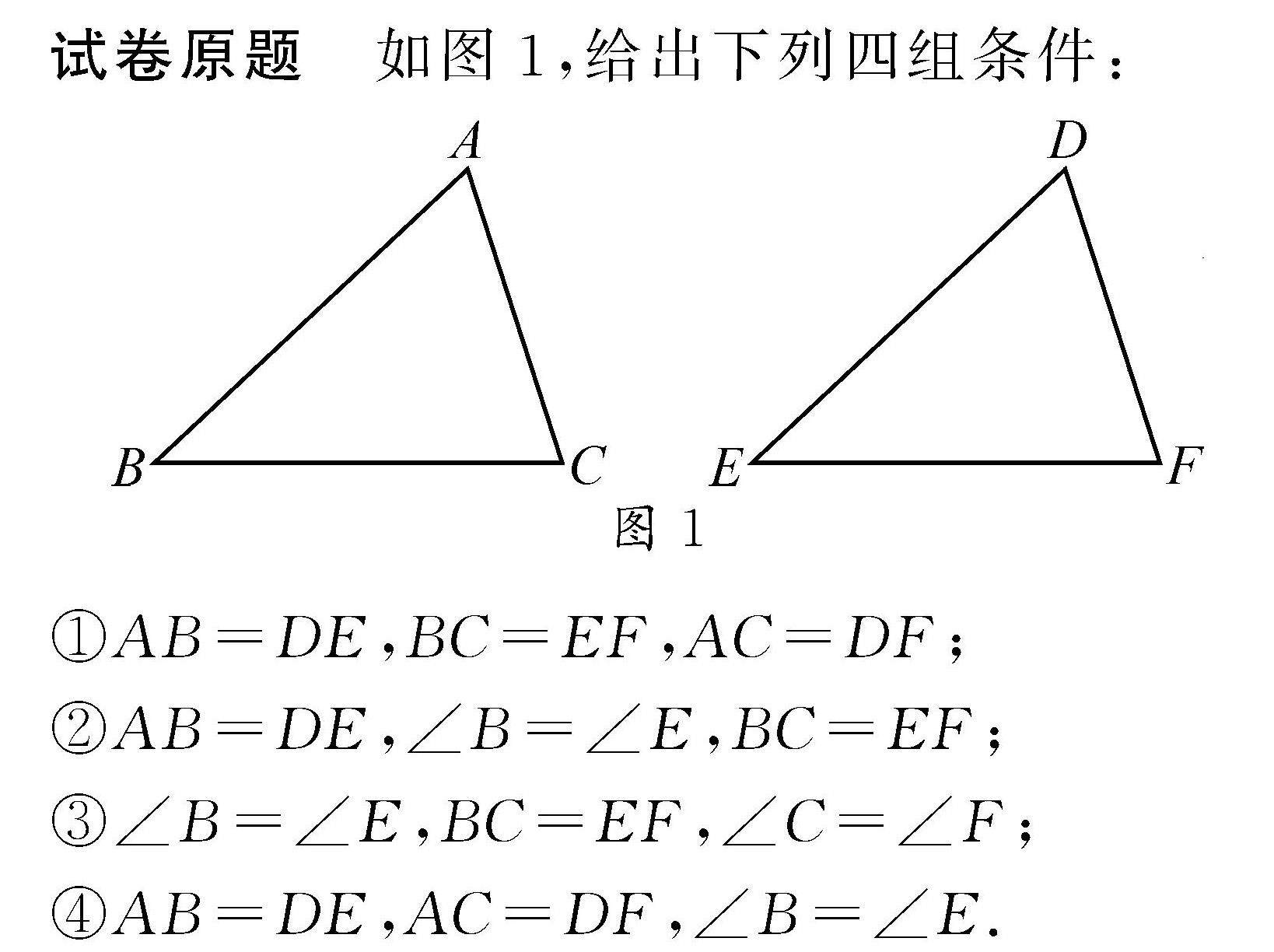
摘要：文中从探究性学习的视角解读初中数学教学内容，在发展学生数学关键能力的框架下，从适切情境、实践活动和合作探究等方面进行探寻，试图研究与把握探究性学习的要素，挖掘蕴含其中的积极效能，利用有效的策略引导学生探索，思考并理解数学本质，进而培养数学关键能力，发展数学核心素养. 关键词：探究性学习；数学关键能力；实践活动 1 问题的提出所谓探究性学习，就是引导学生在一种类似于数学学术研究的情境中
学生学习 | “双减”背景下试卷评讲课的变式训练和能力拓展

学生学习 | “双减”背景下试卷评讲课的变式训练和能力拓展

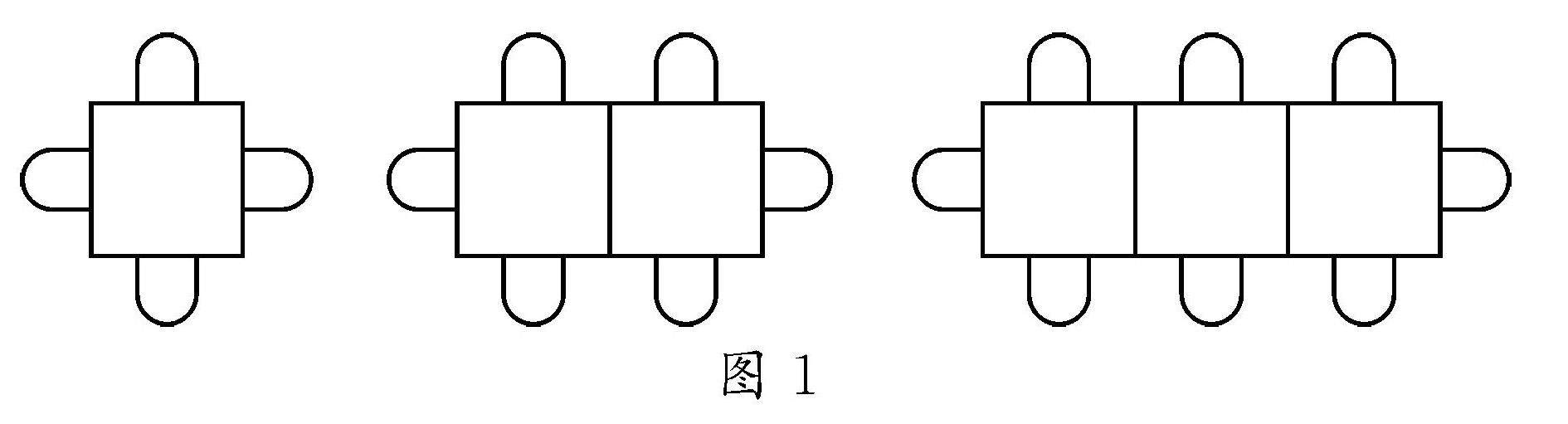
摘要：“双减”要求教师在有效传授知识的同时，更注重学习方法的教授.以一节七年级下册全等三角形的试卷评讲课为例，利用题目的延伸设置引领学生的学习.通过对重点题目的变式训练引导学生更深入地理解和掌握知识点和技巧，再对题目进行拓展，从多个角度让学生重新学习之前没掌握好的知识点，帮助学生学会总结、学会学习. 关键词：试卷评讲；变式训练；题目拓展 “双减”要求教师在有效传授知识的同时，更注重学习方法的传
学生学习 | 设计非书面性作业，发展学生核心素养

学生学习 | 设计非书面性作业，发展学生核心素养

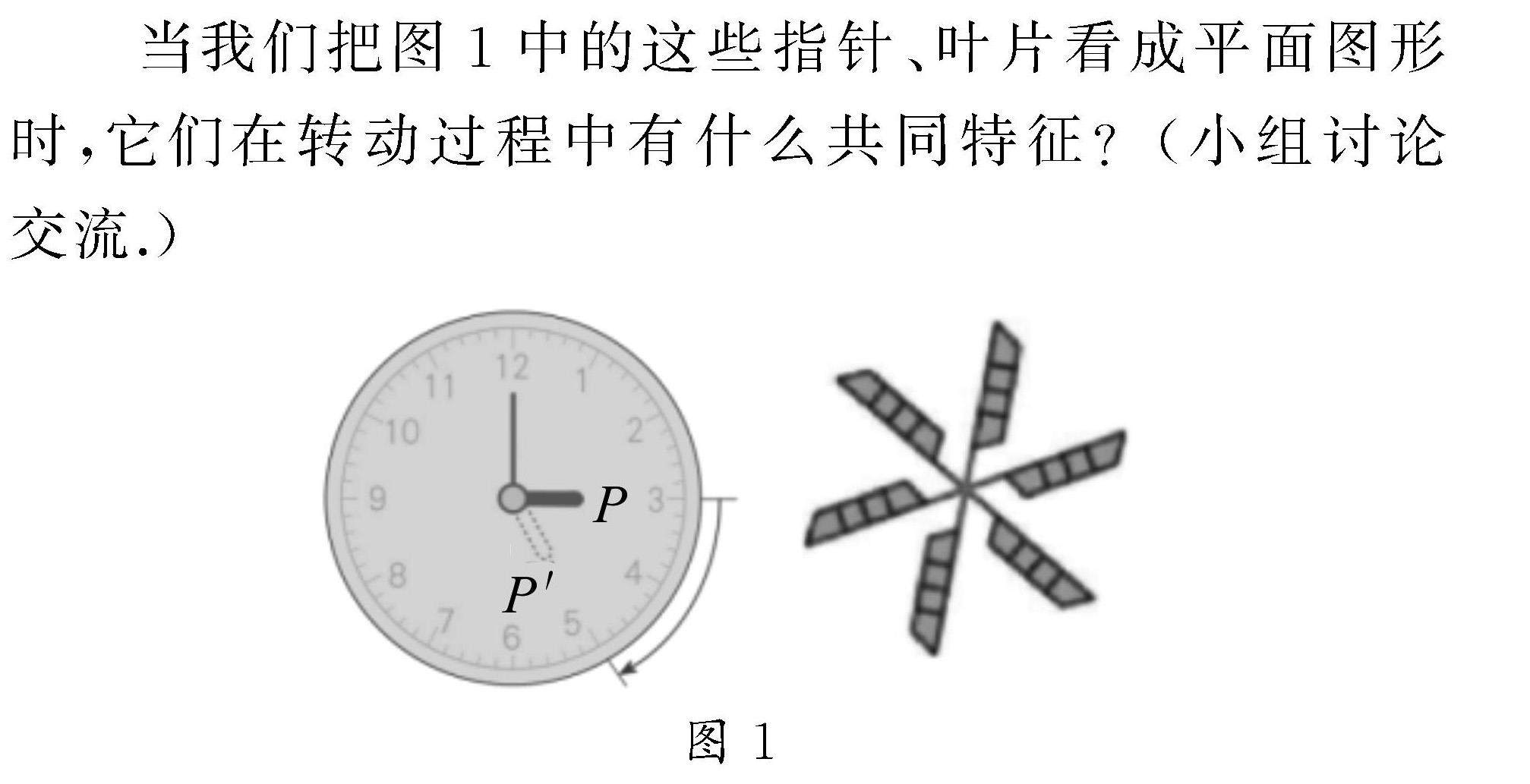
课题信息：江苏省中小学教学研究室第十四期重点自筹课题“基于元认知理论的初中生数学学习力培养研究”，课题编号为2021JY14.ZB143. 摘要：“双减”背景下，减轻学生作业总量是当下数学课堂热议的话题之一.运用好教材中“非书面性作业”资源，开发出指向学生科学素养与学习能力发展的非书面性作业，找准非书面性作业的价值，发展学生的口头表达能力、实践操作能力、活动体验能力以及阅读拓展能力，在有效的策略
学生学习 | 设计探究活动，重视知识生成，落实“三会”素养

学生学习 | 设计探究活动，重视知识生成，落实“三会”素养

合理设置数学探究性活动，激发学生自主探究的欲望和创新思维，引领学生体验，自主观察、发现，善于质疑思考、合作交流，尝试用数学语言表达，发展数学思维能力和认知结构，促使课堂高质量的生成，提高数学素养.本文中以“图形的旋转”为例设计探究活动，谈谈落实“三会”素养的教学尝试. 1 探究活动设计活动1：观察世界，感知概念. 展示图片：在我们的周围存在着很多运动着的物体，请同学们按照它们的运动方式分类
学生学习 | 巧用隐圆解答初中数学最值问题

学生学习 | 巧用隐圆解答初中数学最值问题

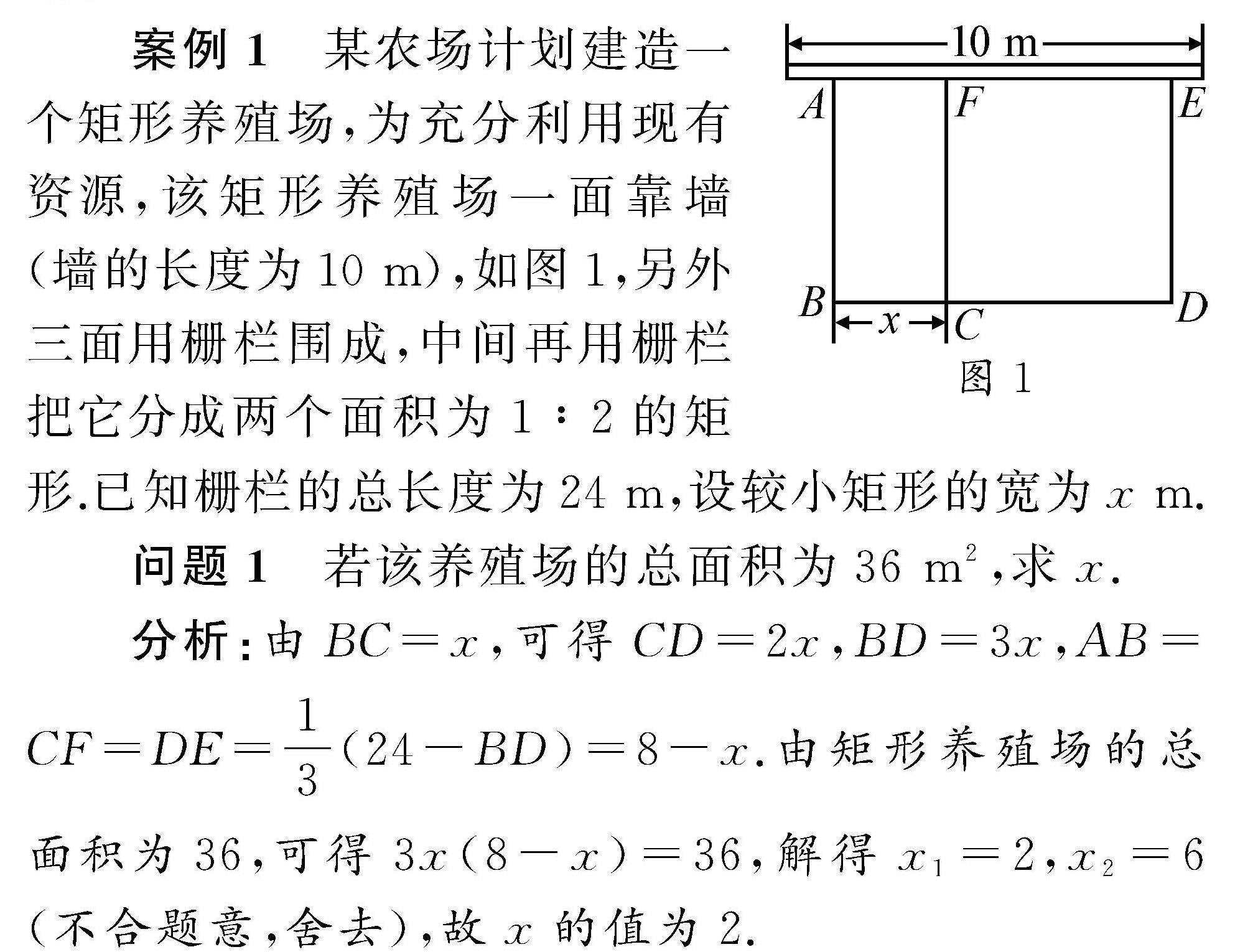
摘要：最值问题是初中数学常见且常考常新的问题之一.巧用隐圆是解答初中数学最值问题的有效方法.本文中介绍了动点定长、直角圆周角、定弦定角、四点共圆四种隐圆情境，结合具体例题展示四种隐圆情境在最值问题中的应用. 关键词：初中数学；隐圆；最值问题隐圆是指题目中并未直接给出圆的图形，需根据对题设条件的判断画出的圆［1］.运用隐圆解答初中数学最值问题的关键在于熟悉隐圆的常见情境，正确迅速找到并画出隐圆
学生学习 | 一题多想，提升初中学生的数学解题能力

学生学习 | 一题多想，提升初中学生的数学解题能力

摘要：教师在数学教学中，要关注学生的思维发展，提升他们解决问题的能力.提升学生解决问题的能力不是让他们机械地多做题目，而是要让他们多思考，促进思维的深度发展.教师可引导学生想一想“是不是还能探究一些问题，是不是有不同的解法，是不是有类似的题目”.通过这样的一题多想，学生的思维能够得到锻炼，解题能力自然能获得发展. 关键词：初中数学；解题能力；一题多想学生在学习数学时不仅要能记住一些基本的知识
学生学习 | 一题多想，提升初中学生探究问题的能力

学生学习 | 一题多想，提升初中学生探究问题的能力

摘要：在初中数学教学中，教师不仅要教授学生各种数学知识和解题方法，还应该注重培养学生探究问题的能力.在实施过程中，教师可以启发学生进行一题多想的探究.本文中结合具体实例，展示了在解决一个问题时可引导学生从“是否可以增加条件、解法或结论”三个方面展开一题多想，以此拓宽学生问题解决的思路和方法. 关键词：一题多想；初中数学；探究问题一题多想，其实就是让学生想出更多的问题，进而促进他们思维的发展.
评价透视 | “双减”背景下初中数学作业设置策略

评价透视 | “双减”背景下初中数学作业设置策略

摘要：“双减”背景下初中数学作业设置，应注重减轻学生的学习负担和素质教育的培养两个方面.作业设置要合理，不能过分增加学生的负担.数学作业的内容应以复习和巩固为主，不宜单纯追求题目的数量，而应注重培养学生的思维能力和解决问题的能力.另外，在结合学科知识的基础上，作业中应融入一些拓展性的内容，培养学生的创新意识和综合应用能力.可以通过设计一些开放性的问题，鼓励学生进行探究和思考，激发学生的学习兴趣和对
评价透视 | 新课标理念下试题命制的基本原则探索

评价透视 | 新课标理念下试题命制的基本原则探索

摘要：新课程标准已于2022年正式实施，对初中数学试题的命制提出了详实、系统、明确的要求，特别是对试题命制的基本原则更具体、明确，有着良好的可操作性.本文中给出了新课标理念下试题命制的三条基本原则. 关键词：试题命制；核心素养；数学智慧；数学创新《义务教育数学课程标准（2022年版）》明确提出了数学核心素养是学生数学学习要实现的根本性目标，规范、严谨、科学命制数学试题是落实这一核心目标的基础
解题天地 | 中考数学不同题型解题思路初探

解题天地 | 中考数学不同题型解题思路初探

中考是初中学生的第一次人生大考，其重要性不言而喻.在分秒必争的考场上，要想快速、准确地答好题，取得满意的成绩，除了要具备扎实的基础知识外，还要选择合理的解题途径，掌握一些行之有效的答题方法与技巧.为此，笔者从选择题、填空题和解答题这三种题型入手，以2022年浙江省杭州市的部分中考试题为例，对中考数学常见的解题思路进行了分析探究，供大家参考. 1 选择题常见的答题思路与技巧选择题在各地市的中考
解题天地 | 例析目标意识在解题中的应用

解题天地 | 例析目标意识在解题中的应用

《义务教育数学课程标准（2022年版）》提出以素养为导向，落实“立德树人”的根本任务.波利亚在《怎样解题》中提出“中学数学首要的任务就是加强解题的训练”，因此培养数学核心素养的重要途径是培养学生的数学解题能力. 目标意识是指对目标重要性的认识，解题活动就是在目标意识的监控下进行的有目的的思维过程.但在应试教育的影响下，许多教师不能将解题的重点放在分析目标上，而是将大量时间花费在技巧归类、总结题型
解题天地 | 尝试多种解法培养创新素养

解题天地 | 尝试多种解法培养创新素养

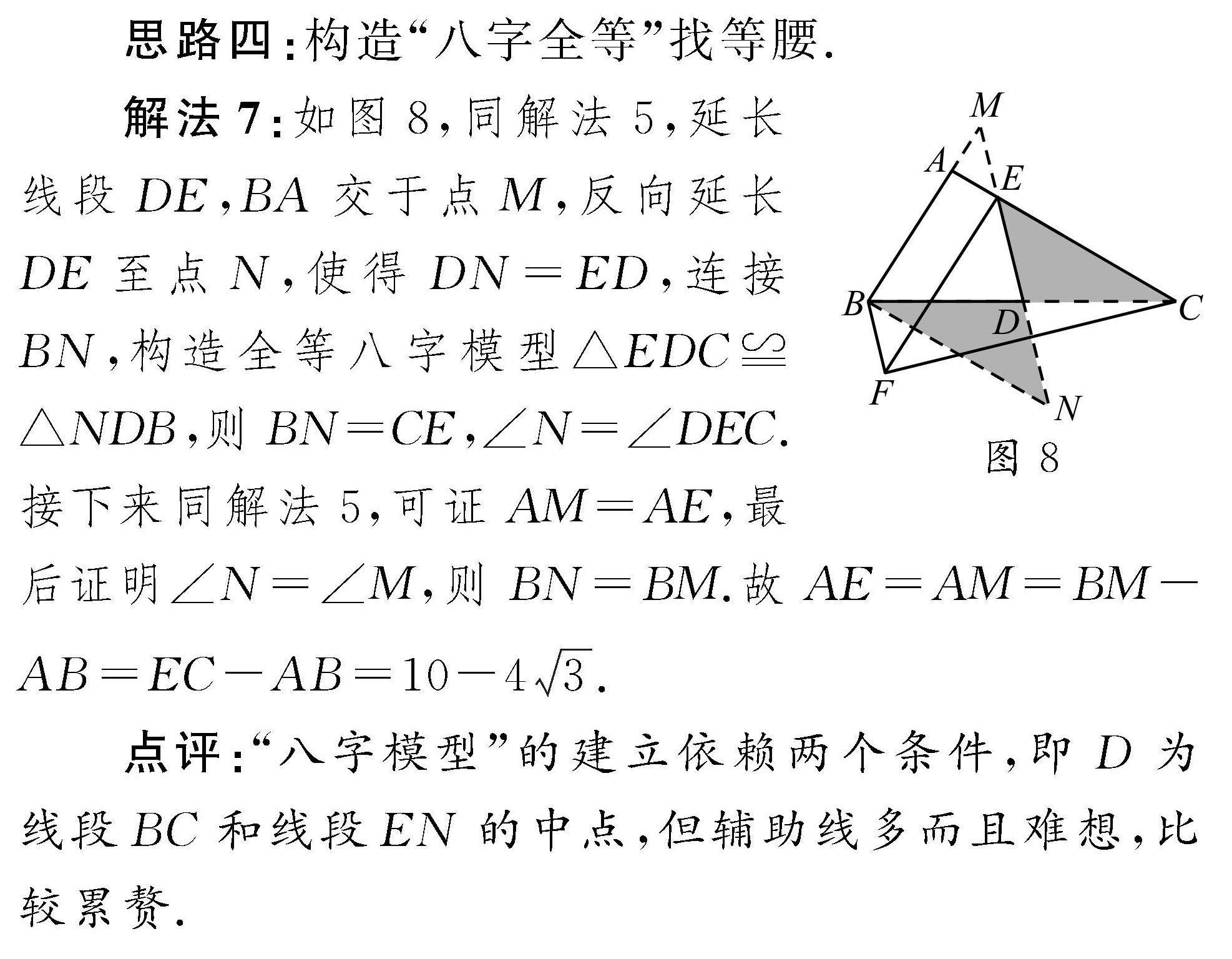
摘要：培养创新素养是《义务教育数学课程标准（2022年版）》中的任务要求.因此，培养学生的创新精神、创新意识、创新能力是我国教育的需求，将创新素养融入平时的教学是落实要求的有力方式.本文中以一道几何证明题为例，展开多种方法的分析，发展学生的理性思维，培养学生的创新意识，落实数学核心素养. 关键词：创新意识；中考压轴；一题多解 1 试题呈现例如图1，过弦AB的一端点B作一切线BC，过另一
解题天地 | 展折叠之美，育思维之花

解题天地 | 展折叠之美，育思维之花

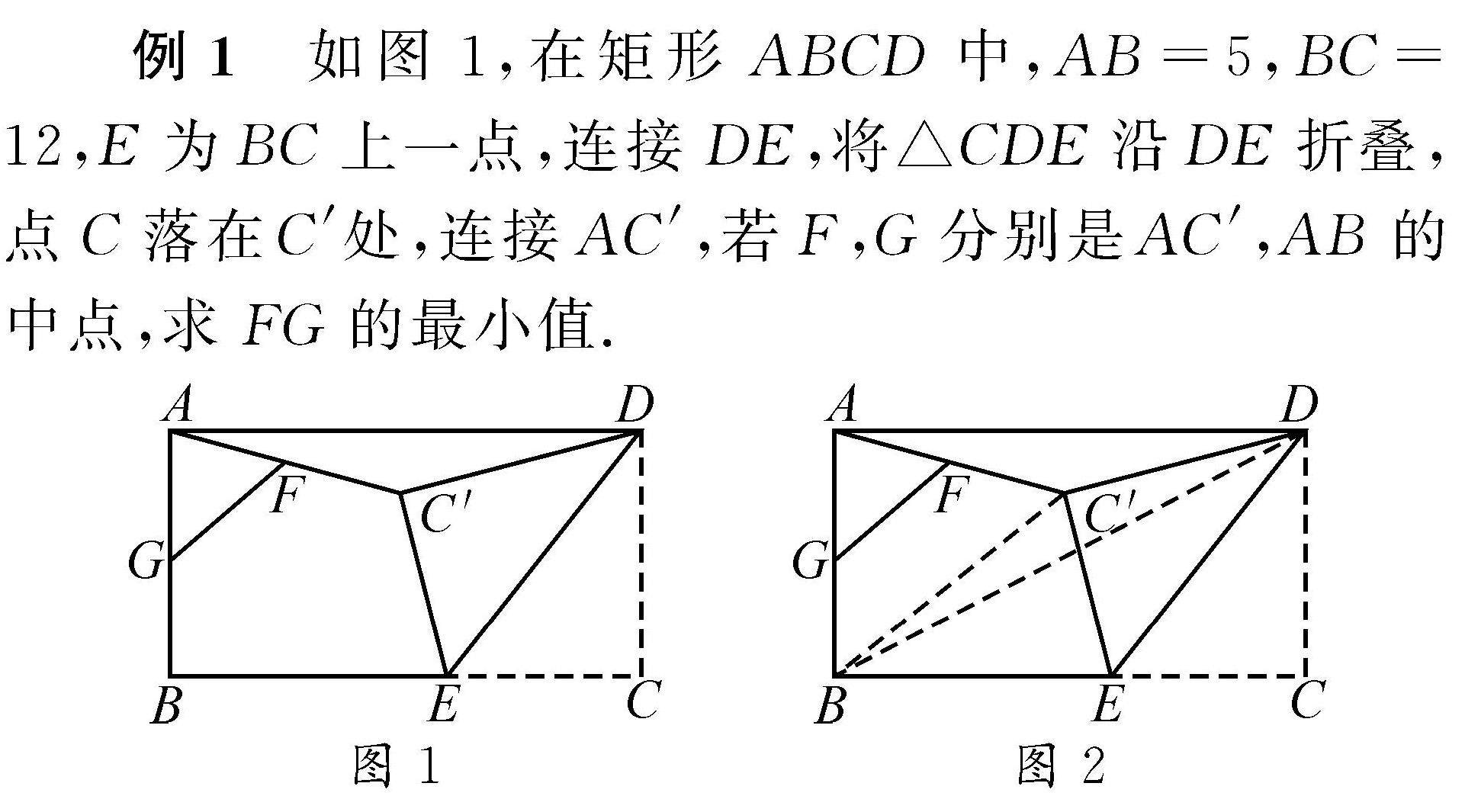
折叠问题是中考数学的高频考点，深圳中考也不例外.折叠问题主要分直接计算型和分类讨论型两大类题型，由浅入深，难度逐渐加大.2021年是深圳新中考第一年，数学试题的难度一度上了热搜.很多学生反映“题目很新”“题目很难”等.具体真相如何？我们一起来揭开填空压轴题的真面目，感受数学之趣、数学之美，提升数学素养. 1 真题呈现如图1所示，在△ABC中，AB=43，D，E分别为线段BC，AC上一点，EC
解题天地 | 由一道中考压轴题联想到的“最值”求解策略

解题天地 | 由一道中考压轴题联想到的“最值”求解策略

摘要：最值问题是近几年来中考数学命题的热点之一，其考查方式也是多种多样，更是多元化的，问题展示过程灵活，综合性强，是考查学生分析问题和解决问题能力的主要题型.本文中就连云港市中考填空压轴试题的剖析，针对初中阶段出现的几种最值问题进行策略分析研究. 关键词：初中数学；中考压轴；最值；求解策略 “最值问题”是近年来中考数学的必考题型，也是压轴题中的必选之题.遇到此类问题，学生往往无从下手，掌握此类
解题天地 | 活用辅助线，巧妙建立联系

解题天地 | 活用辅助线，巧妙建立联系

在初中数学教学体系中，利用几何知识解题历来是一块“难啃的骨头”.在这一背景下，学生唯有掌握辅助线的应用技巧，合理构造辅助线，才能构建出全新的条件，扫清解题中的障碍.构建必要的辅助线，不仅能够揭示图形的本质，帮助学生更好地探索图形背后的性质，还可以借助辅助线增强学生的问题分析能力，发展学生的空间观念等数学核心素养.基于此，结合新课程标准的要求，鉴于学生解题的需求，培养学生构建辅助线的能力已经成为一项
解题天地 | 一道复合型路径问题的探究

解题天地 | 一道复合型路径问题的探究

动点的路径问题是中考的一个难点，尤其是复合型路径问题，即直线型路径和圆弧型路径的综合.破解这类试题的关键就是抓住变化中的不变量，从几何关系入手.下面结合一道经典试题来分析复合型路径问题的解决方法与思路［1］. 1 试题呈现如图1，已知抛物线y=ax2+bx+74过A（1，0），B（7，0）两点，且与y轴相交于点D.现以线段AB为边在x轴上方作等边三角形ABC. （1）求抛物线的解析式.
解题天地 | 方程与不等式代数综合推理题的剖析

解题天地 | 方程与不等式代数综合推理题的剖析

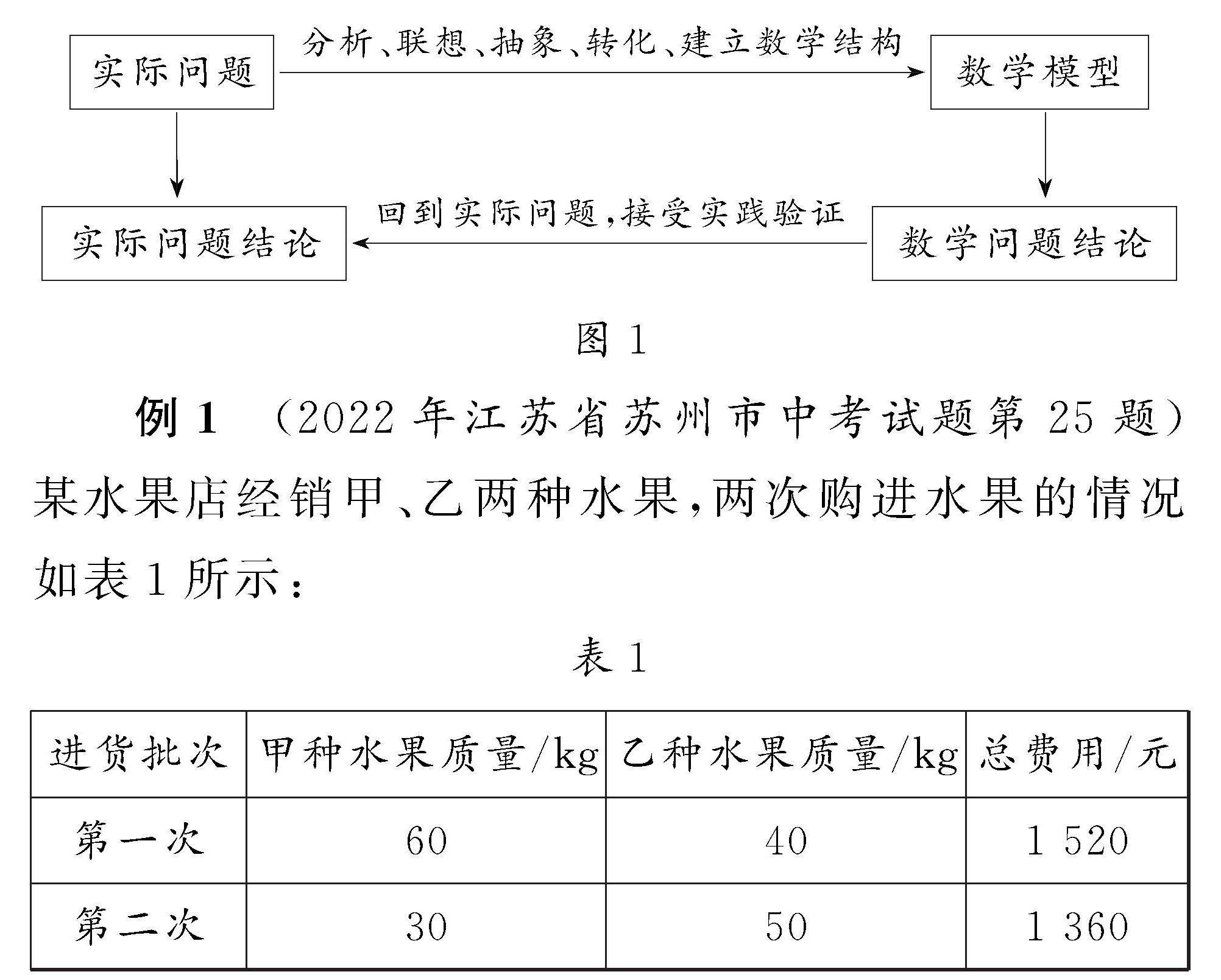
一元一次方程与一元一次不等式是初中代数最基础的知识，学生一般对它们的解法都能够熟练掌握，但将二者结合后，情况就不尽如人意了．下面结合实例，剖析一次方程与不等式综合的代数推理题的解法． 1 求取值范围例1 （1）已知x-y＝4，且x＞3，y＜1，求x＋y的取值范围．（2）关于x，y的方程组3x-y=2a-5，x+2y=3a+3的解都是正数，若a-b＝4且b＜2，求a＋b的取值范围．解
解题天地 | 运用转化思想解决初中函数应用题

解题天地 | 运用转化思想解决初中函数应用题

近几年各地的中考数学试题中，出现了一些设计新颖、贴近生活、反映时代特点的函数应用题.实际问题来源于生活，这些问题的解答要依赖于众多的数学思想和答题技巧.如函数思想、方程思想、数形结合思想和转化思想，其中转化思想贯穿解题的始终［1］.具体来说，就是把具体实际问题转化为数学中的函数问题，把众多的变量（未知量）转化成用一个变量（或已知量）来表示，把复杂问题转化成一个或多个简单问题. 1 题型一：利用一
解题天地 | 数形结合思想在反比例函数解题中的应用

解题天地 | 数形结合思想在反比例函数解题中的应用

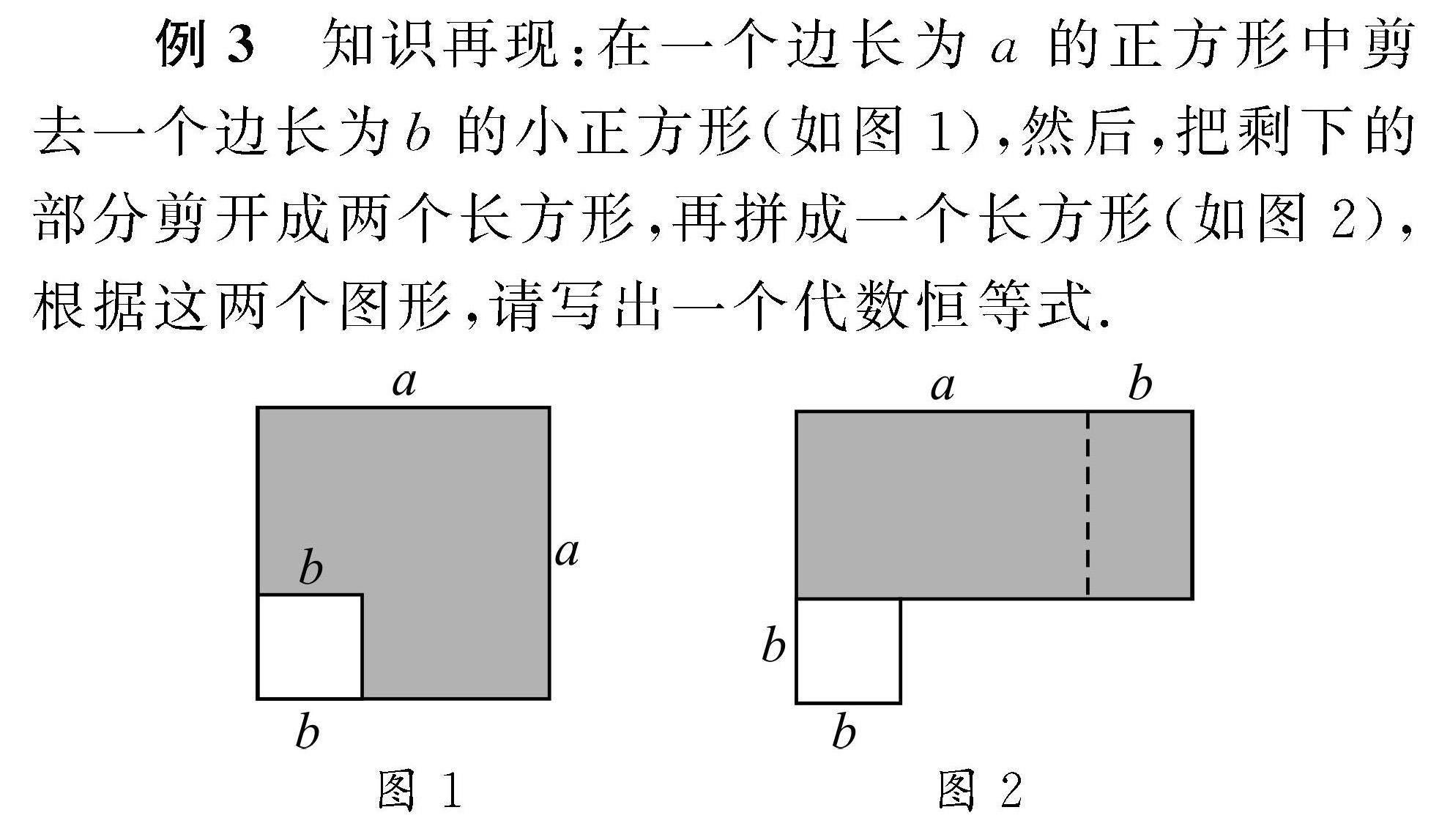
摘要：数形结合是非常重要的数学思想之一，描述了“数”与“形”两个重要对象的密切联系.初中阶段，用数形结合思想解答的习题情境也是常考常新.反比例函数是初中数学非常重要的函数类型，相关题型灵活多变.数形结合思想可给反比例函数习题的解答带来良好指引，从而提高解题效率.为深化学生对数形结合思想的进一步认识，帮助学生积累相关的运用技巧，提高运用数形结合思想的意识与能力，本文中展示了数形结合思想在不同反比例函
解题天地 | 因式分解的拓展探究

解题天地 | 因式分解的拓展探究

因式分解是初中数学的重要知识点，中考专门考查这一知识点的试题并不多，主要渗透在其他试题的考查中.本文中主要从因式分解与最值、新定义、图形体积、换元法等方面说明中考中对因式分解的拓展考查. 1 因式分解与最值利用因式分解求最值，通常是指将一个二次三项式配方出一个完全平方式，然后根据（a±b）2一定是非负数求得最值.当多项式配方为a（x±b）2+c时，此多项式一定有最小值c，此时完全平方式为0；
教师发展 | 你遇到过这“尴尬”的一幕吗？

教师发展 | 你遇到过这“尴尬”的一幕吗？

在讲解反比例函数习题的过程中，笔者曾两次遇到“尴尬”的一幕，课堂上有学生表示：“老师，您的方法太烦了，我有简便方法.”虽然我硬着头皮讲完，但学生之后展示的方法确实比我的简单，作为教师的我都有点汗颜.在之后的章节测试中，笔者发现大多数学生虽然在课堂上对那位同学的方法赞叹不已，但最终还是运用了老师讲的方法解决问题.这一经历促使笔者深入思考“通性通法”与“特解巧法”的关系. 1 第一次教学经历如图
教师发展 | 问题引领思维，赋能智力提升

教师发展 | 问题引领思维，赋能智力提升

摘要：教师要想从真正意义上启迪学生智慧，就需要以“问题”为媒介，引领深入、深刻与深度的数学思考，让思维真正成为数学学习的灵魂，为智力提升赋能.本文中结合案例阐述了以精设悬疑类问题、故事类情境、实践性问题和开放性问题助推思维拔节的实施策略. 关键词：问题；数学思维；课堂教学众所周知，思维是智力活动中各种因素的“支配者”，唯有在思维的真实参与下，一切智力活动才是真实有效的，数学学习更是如此.因此
教师发展 | 课堂教学中“错误”的价值生长

教师发展 | 课堂教学中“错误”的价值生长

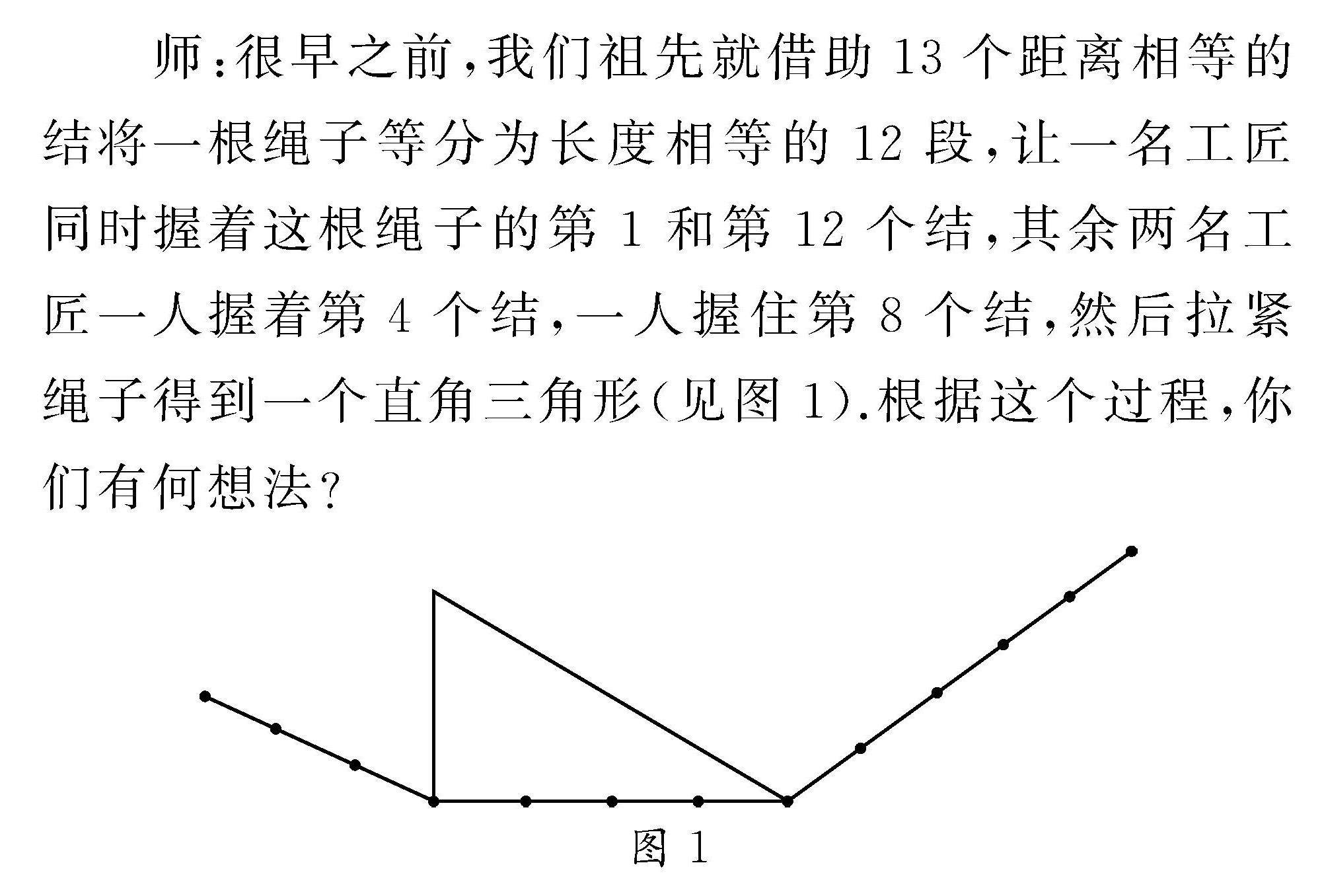
摘要：数学课堂中不可避免地会生成这样或那样的“错误”.文章以“探索勾股定理”的部分教学片段为例，对课堂教学中的“错误”进行了描述和分析，并探讨了“错误”对于教学的意义，同时提出了用教师的教学智慧去呵护“错误”和化解“错误”，让学生在纠错中体会成功的艰辛，感受探究的快乐，收获成功的喜悦. 关键词：错误；教学智慧；课堂教学 1 问题提出教学智慧是大智慧的自然呈现，也是综合素养的集中反映.新课程
教师发展 | 初中数学课堂教学效率的提升点

教师发展 | 初中数学课堂教学效率的提升点

摘要：数学教学中需要融入教师的教学艺术，高效利用课堂，为学生的自主建构和思维发展搭桥铺路，让学生产生要学、会学、爱学的积极情感，以提升课堂教学效率.文章认为，教师在构思教学时需设计适切导入策略，引发深入思考；创设精当问题情境，引领合作探究；设计有效课堂练习，培养高阶思维.这样才能从根本上提升教学效率，培养学生的数学核心素养. 关键词：课堂导入；问题情境；课堂练习；教学效率细细体味数学教学的意
教师发展 | 创设教学高潮，提升教学效率

教师发展 | 创设教学高潮，提升教学效率

摘要：在初中数学教学中，为了更好地发展学生，教师应该结合教学实际创设教学情境，灵活运用冲突、矛盾、竞争、悬念等活动将课堂教学引入高潮，以此充分发挥学生的主体价值，激活学生的思维，培养学生良好的思考习惯，提高课堂教学有效性. 关键词：发展学生；数学活动；高潮在教学“平行四边形”时，笔者曾经有过这样一个经历：在课堂教学中，通过直接讲授与合作学习相结合的方式让学生理解并掌握了平行四边形的概念及边、
教师发展 | 创新讲题形式，提升学生讲题能力

教师发展 | 创新讲题形式，提升学生讲题能力

摘要：学生讲题是让学生参与试题分析和讲解的方式，有效地落实学生的主体地位，提升学生参与学习活动的积极性，对于发展学生的思维品质具有积极作用.本文中从基础性试题、创新性试题、发展性试题、挑战性试题四个层面分析组织学生讲题的策略，以提升课堂教学的有效性. 关键词：学生讲题；思维能力；学习成就学生讲题是指让学生作为“小老师”分析讲解试题，梳理解题思路，提炼解题方法等，是在师生互动交流的过程实现知识
教师发展 | 用信息化手段突破数学课堂教学的抽象性

教师发展 | 用信息化手段突破数学课堂教学的抽象性

摘要：数学学科讲究逻辑，其学习内容具有一定的抽象性，随着学段的提升，学生接触的数学课程内容的抽象程度也会随之提升.数学课程内容的抽象性已经成为很多学生在学习数学道路上的“拦路虎”，因此突破初中数学抽象性具有重要意义.目前，在信息技术的支持下，基于几何画板、多媒体、AR技术和学情分析，通过融合信息化手段、创新教学设计，实现教育信息化2.0背景下的教学改革目标，使初中数学教学进一步实现提质增效. 关

过往期刊

更多

猜你喜欢

苏州工业园区教育局电子阅览室