目录
快速导航-

课程教材教法 | 借力微教研 锤炼教学观
课程教材教法 | 借力微教研 锤炼教学观
-

课程教材教法 | 基于ACT-R理论的“高中数学探究活动”教学实践与思考
课程教材教法 | 基于ACT-R理论的“高中数学探究活动”教学实践与思考
-

课程教材教法 | 在数学教育视角下发展学生的高阶思维
课程教材教法 | 在数学教育视角下发展学生的高阶思维
-

课程教材教法 | 知识内容组织视角下两人教A版教材的比较分析
课程教材教法 | 知识内容组织视角下两人教A版教材的比较分析
-

课例评析 | HPM视角下“等差数列前n项和公式”的教学
课例评析 | HPM视角下“等差数列前n项和公式”的教学
-

课例评析 | 指向深度学习的单元教学活动设计
课例评析 | 指向深度学习的单元教学活动设计
-

课例评析 | 让学生经历定理学习的完整过程
课例评析 | 让学生经历定理学习的完整过程
-

教学实践 | 探索知识形成过程 提升数学抽象素养
教学实践 | 探索知识形成过程 提升数学抽象素养
-

教学实践 | 精心设计 提升素养
教学实践 | 精心设计 提升素养
-

教学实践 | 问题驱动探究 实验启发思维
教学实践 | 问题驱动探究 实验启发思维
-

教学实践 | 高中数学课程思政元素切入点的探索与实践
教学实践 | 高中数学课程思政元素切入点的探索与实践
-

教学实践 | APOS理论与变式教学理论深度融合的实践与研究
教学实践 | APOS理论与变式教学理论深度融合的实践与研究
-

教学实践 | 指向核心素养发展的教材“再建构”研究
教学实践 | 指向核心素养发展的教材“再建构”研究
-

教学实践 | 让“意外”成为课堂动态生成的资源
教学实践 | 让“意外”成为课堂动态生成的资源
-

教学实践 | 关注基础 统筹规划 提升素养
教学实践 | 关注基础 统筹规划 提升素养
-

教学实践 | 对高效教学设计的思考与实践
教学实践 | 对高效教学设计的思考与实践
-
教学实践 | 促进数学建模的高中数学项目化学习案例研究
教学实践 | 促进数学建模的高中数学项目化学习案例研究
-

教学实践 | 合理设计微专题 提升教学有效性
教学实践 | 合理设计微专题 提升教学有效性
-

教研在线 | 走出“机械刷题” 走进“深度学习”
教研在线 | 走出“机械刷题” 走进“深度学习”
-

教研在线 | 概念教学中过程性评价的着眼点
教研在线 | 概念教学中过程性评价的着眼点
-

教研在线 | GeoGebra软件在可视化教学中的应用研究
教研在线 | GeoGebra软件在可视化教学中的应用研究
-
教研在线 | 基于数学学科核心素养培养高中生阅读能力的研究
教研在线 | 基于数学学科核心素养培养高中生阅读能力的研究
-
教研在线 | “三会”素养导向下高中数学跨学科教学实践研究
教研在线 | “三会”素养导向下高中数学跨学科教学实践研究
-

教研在线 | 关于“距离的计算”章节知识内容的教学指导与思考
教研在线 | 关于“距离的计算”章节知识内容的教学指导与思考
-

教研在线 | 关于圆锥曲线证明题探究的教学指导
教研在线 | 关于圆锥曲线证明题探究的教学指导
-

教学反思 | 对上好习题课的几点认识
教学反思 | 对上好习题课的几点认识
-

教学反思 | 对提高试卷讲评课有效性的思考与实践
教学反思 | 对提高试卷讲评课有效性的思考与实践
-

教学反思 | 对如何培养学生创造力的思考与实践
教学反思 | 对如何培养学生创造力的思考与实践
-

教学技巧 | 尊重差异 因材施教
教学技巧 | 尊重差异 因材施教
-

教学技巧 | 指向核心素养的数学概念教学探索
教学技巧 | 指向核心素养的数学概念教学探索
-
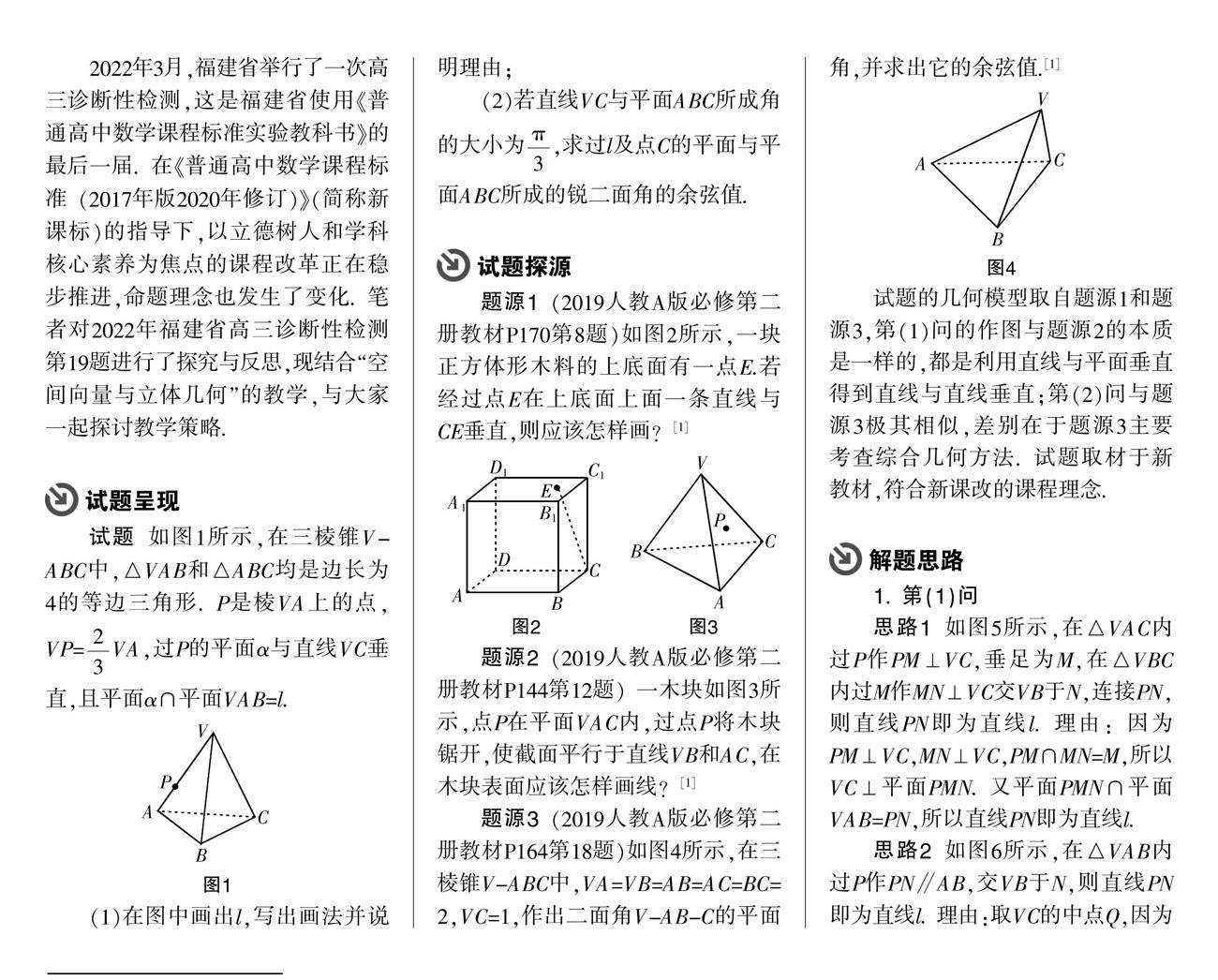
试题研究 | 溯教材之源,探直观想象培养
试题研究 | 溯教材之源,探直观想象培养
-

试题研究 | 用对称和迭代的思想求切线方程
试题研究 | 用对称和迭代的思想求切线方程
-

试题研究 | 问题解读多解探索,方法总结应用拓展
试题研究 | 问题解读多解探索,方法总结应用拓展



















 登录
登录