全部分类/
中学教育/
中学生数理化·高一数学

中学生数理化·高一数学

2024年05期

本刊由河南教育报刊社主管主办，经国家新闻出版总署批准的省级纯教育类刊物，中国期刊方阵双百期刊，具有国际国内双刊号的教育学术权威期刊，面向国内外公开发行。

扫码免费借阅

知识结构与拓展 | 总体百分位数的估计

知识结构与拓展 | 总体百分位数的估计

总体百分位数的估计是新教材增加的内容，直观上比较容易理解，它把一组按大小排列的数据分成相应百分比的两部分，一组数据的第p 百分位数是这样一个值，它使得这组数据中至少有p%的数据小于或等于这个值，且至少有（1-p）%的数据大于或等于这个值。几种常用的百分位数：第25百分位数（又称下四分位数或第一四分位数），第50百分位数（又称中位数或第二四分位数），第75百分位数（又称上四分位数或第三四分位数），第
知识结构与拓展 | 一个频率分布直方图问题的变式探究

知识结构与拓展 | 一个频率分布直方图问题的变式探究

基于新课标、新教材、新高考的“三新”背景，学好数学不能停留在“题海”上，这是新课标所倡导的方向。如果同学们对做过的题目没有认真思考和深入探究，做再多的题也不会达到预期的效果。只有进一步的探究，才能得到理想的学习效果，由此可得到一些新的结论，深层次地进行知识的应用。下面结合一个常见的频率分布直方图问题进行变式与应用。题目有一个容量为200的样本，其频率分布直方图如图1所示，根据样本的频率分布直
知识结构与拓展 | 利用频率分布直方图估计总体的数字特征

知识结构与拓展 | 利用频率分布直方图估计总体的数字特征

借助频率分布直方图，可以估计总体的数字特征，从而对数据进行有效分析。一、利用频率分布直方图估计平均数在频率分布直方图中，平均数的估计值等于每个小矩形底边中点的横坐标（组中值）与相应频率（小矩形的面积）的乘积之和。例1 某校对100名高一学生的某次数学测试成绩进行统计，分成[50，60），[60，70），[70，80），[80，90），[90，100]五组，得到如图1所示的频率分布直方图
知识结构与拓展 | 方差的巧妙计算与应用

知识结构与拓展 | 方差的巧妙计算与应用

方差（或标准差）是用来描述一个样本和总体的波动情况的统计量，用方差（或标准差）可以判断样本数据的分散程度的大小，方差越大（或越小），样本数据的离散程度越大（或越小）。在实际应用过程中，利用方差的计算公式及对应的变形公式，对于解决一些与方差相关的数学应用问题往往有奇效。
知识结构与拓展 | 分层抽样题型例析

知识结构与拓展 | 分层抽样题型例析

分层抽样是常用的抽样方法之一。分层抽样的常见题型：求样本容量，求总体容量，求层中样本容量，分层抽样的应用等。下面分类解析。
知识结构与拓展 | 事件的相互独立性的诠释与应用

知识结构与拓展 | 事件的相互独立性的诠释与应用

一、事件的相互独立性 1.相互独立的概念一般地，若事件A，B 满足P （AB ）=P（A）P（B），则称事件A 与B 相互独立。（1）事件A 与事件B 独立是相互的。（2）设A 与B 为两个事件，则下列四对事件：A 与B、A 与B，A 与B，A 与B，只要有一对事件相互独立，其余三对也相互独立。（3）若事件B 发生与否对事件A 发生的概率没有影响，则事件A，B 独立。 2.互斥
知识结构与拓展 | 记住概率中的八个“事件”

知识结构与拓展 | 记住概率中的八个“事件”

事件是研究概率问题的基本单位，求解概率问题要熟记八个“事件”，要弄清各自的特征。一、基本事件例1 已知集合M = {-2，3}，N ={-4，5，6}，从这两个集合中各取一个元素分别作为点的横、纵坐标，则这个试验的基本事件的总数为____。解：由题意得试验的基本事件空间Ω ={（-2，-4），（-2，5），（-2，6），（3，-4），（3，5），（3，6），（-4，-2），（-4，3
知识结构与拓展 | 例析分层随机抽样的常见题型

知识结构与拓展 | 例析分层随机抽样的常见题型

分层随机抽样是随机抽样的一种重要方法，使用的前提是总体可以分层，层与层之间有明显区别，而层内个体间差异较小，每层中所抽取的个体数可按各层个体数在总体上所占的比例抽取。分层随机抽样要求对总体有一定了解，明确分层的界限和数目，只要分层恰当，一般来说抽样结果比简单随机抽样更能反映总体情况。下面就分层随机抽样的常见题型进行举例分析，供大家学习与提高。一、基本概念或基本性质问题例1 为了保证分层随机
知识结构与拓展 | 记住统计中的五个“数”

知识结构与拓展 | 记住统计中的五个“数”

众数、中位数、平均数、百分位数和频数是统计数据的重要特征数，主要描述数据的集中趋势。一、众数例1 为了弘扬体育精神，某校组织秋季运动会，在一项比赛中，学生甲进行了8组投篮，得分分别为10，8，5，8，7，9，6，8，则这组数据的众数为____。解：因为数据10，8，5，8，7，9，6，8中出现次数最多的是8，所以这组数据的众数为8。评注：在一组数据中，出现次数最多的数据就是这组数据
数学文化与赏析 | 统计中的核心素养

数学文化与赏析 | 统计中的核心素养

随机抽样是从总体中抽取样本，借助频率分布表画出频率分布直方图，可以提升数据分析和读图的能力，凸显直观想象、数据分析的核心素养。从样本数据中提取样本的数字特征（如平均数、标准差），并做出合理的解释，凸显数学运算的核心素养。用样本的频率分布估计总体分布，用样本的基本数字特征估计总体的基本数字特征，凸显数学建模的核心素养。题型一：简单随机抽样例1 （1）“嫦娥五号”的成功发射，实现了中国航天史上
核心考点演练 | 统计核心考点综合演练

核心考点演练 | 统计核心考点综合演练

一、选择题 1.下列调查方式合适的是（）。 A.为了解一批炮弹的杀伤半径，采用普查的方式 B.为了解一批玉米种子的发芽率，采用普查的方式 C.为了解一条河流的水质，采用抽样调查的方式 D.为了解一个寝室的学生（共5个人）每周体育锻炼的时间，采用抽样调查的方式 2.已知甲、乙两组按顺序排列的数据，甲组：27，28，37，m ，40，50;乙组：24，n，34，43，48，52。若这两组
核心考点演练 | 概率核心考点综合演练

核心考点演练 | 概率核心考点综合演练

一、选择题
易错题归类剖析 | 立足基础　常考常新

易错题归类剖析 | 立足基础　常考常新

概率是每年高考的重点考查内容之一，尤其是简单的古典概型问题。在日常工作和社会经济生活中，有大量的随机事件的概率并不一定要通过大量的试验来得到，只要知道了一些基本情况，就可以知道它们相应的概率，这就是最常见的古典概型。下面就古典概型中常见的易错点进行剖析，使同学们达到“误”中有“悟”。一、基本事件的确定问题例1 从13张黑桃的扑克牌中，任意取出1张，它是花牌的概率是多少？错解：因为抽出的
易错题归类剖析 | 统计典型易错点剖析

易错题归类剖析 | 统计典型易错点剖析

易错点1：忽视中位数需从小到大排序（2）由分层抽样法可得，在销售量为13t的天数中应抽取20× 10／100=2，在销售量为14t的天数中应抽取20×40／100=8，在销售量为15t的天数中应抽取20×20／100=4，在销售量为16t的天数中应抽取20×20／100=4，在销售量为17t的天数中应抽取20× 10／100=2。故销售量为13t，14t，15t，16t，17t中，取出的天数分
创新题追根溯源 | 聚焦古典概型的交汇问题

创新题追根溯源 | 聚焦古典概型的交汇问题

古典概型与其他知识的交汇问题，应根据相关知识点，构建有序实数对，列举出所有的基本事件和满足条件的基本事件，进而根据古典概型的公式求解。
创新题追根溯源 | 2023年高考统计问题聚焦

创新题追根溯源 | 2023年高考统计问题聚焦

2023年高考统计问题主要围绕样本的数字特征、抽样方法、用样本估计总体、变量间的相关关系、独立性检验、统计与概率的交汇展开，其中数字特征、随机抽样和总体估计是高考的常考点，一般以选择题或填空题的形式出现。高考考查凸显数学建模及数据分析的核心素养。
经典题突破方法 | 统计常见典型考题赏析

经典题突破方法 | 统计常见典型考题赏析

题型一：分层抽样分层随机抽样中按比例分配计算时，用到的两个关系式：样本容量n／总体个数N =该层抽取的个体数／该层的个体数;总体中某两层的个体数之比等于样本中这两层抽取的个体数之比。用样本平均数估计总体平均数：在分层随机抽样中，若第一层的样本容量为m ，平均值为x，第二层的样本容量为n，平均值为y，则样本的平均值为mx+ny／m +n 。例1 某公司有大量客户，且不同年龄段客户对其服务的
经典题突破方法 | 2023年高考概率经典问题聚焦

经典题突破方法 | 2023年高考概率经典问题聚焦

2023年高考对概率的考查主要围绕古典概型，几何概型，相互独立事件等问题展开，凸显概率的工具性、应用性和“数学建模，数据收集，逻辑推理与计算”等核心素养。
经典题突破方法 | 概率常见典型考题赏析

经典题突破方法 | 概率常见典型考题赏析

概率是高中新教材中的重要内容之一，也是高考的常考内容。高考主要考查随机事件的关系，考查古典概率、对立事件的概率、概率与其他知识的交汇等。下面就概率中的典型考题进行举例分析，供大家学习与参考。题型1：随机事件的关系互斥事件与对立事件的区别与联系：互斥事件是不可能同时发生的事件，但也可以同时不发生;对立事件是特殊的互斥事件，特殊在对立的两个事件不可能都不发生，即有且仅有一个发生。例1 设条

中学生数理化·高一数学

目录

知识结构与拓展 | 总体百分位数的估计

知识结构与拓展 | 总体百分位数的估计

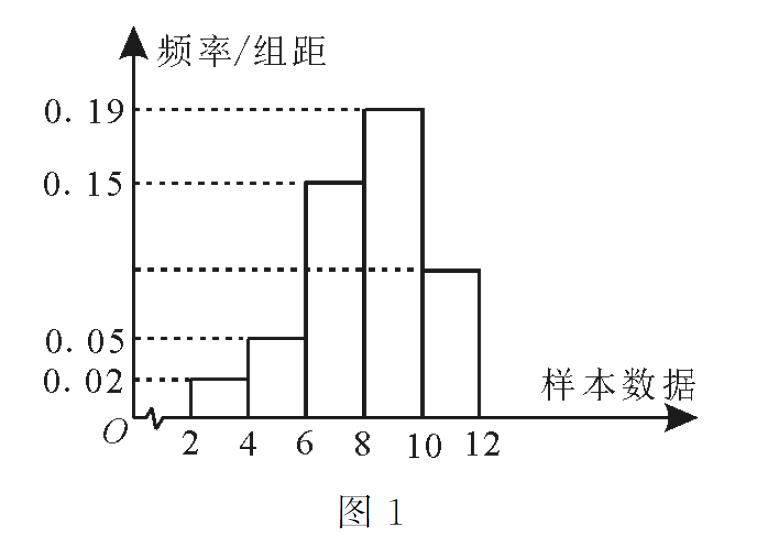
知识结构与拓展 | 一个频率分布直方图问题的变式探究

知识结构与拓展 | 一个频率分布直方图问题的变式探究

知识结构与拓展 | 利用频率分布直方图估计总体的数字特征

知识结构与拓展 | 利用频率分布直方图估计总体的数字特征

知识结构与拓展 | 方差的巧妙计算与应用

知识结构与拓展 | 方差的巧妙计算与应用

知识结构与拓展 | 分层抽样题型例析

知识结构与拓展 | 分层抽样题型例析

知识结构与拓展 | 事件的相互独立性的诠释与应用

知识结构与拓展 | 事件的相互独立性的诠释与应用

知识结构与拓展 | 记住概率中的八个“事件”

知识结构与拓展 | 记住概率中的八个“事件”

知识结构与拓展 | 例析分层随机抽样的常见题型

知识结构与拓展 | 例析分层随机抽样的常见题型

知识结构与拓展 | 记住统计中的五个“数”

知识结构与拓展 | 记住统计中的五个“数”

数学文化与赏析 | 统计中的核心素养

数学文化与赏析 | 统计中的核心素养

核心考点演练 | 统计核心考点综合演练

核心考点演练 | 统计核心考点综合演练

核心考点演练 | 概率核心考点综合演练

核心考点演练 | 概率核心考点综合演练

易错题归类剖析 | 立足基础 常考常新

易错题归类剖析 | 立足基础 常考常新

易错题归类剖析 | 统计典型易错点剖析

易错题归类剖析 | 统计典型易错点剖析

创新题追根溯源 | 聚焦古典概型的交汇问题

创新题追根溯源 | 聚焦古典概型的交汇问题

创新题追根溯源 | 2023年高考统计问题聚焦

创新题追根溯源 | 2023年高考统计问题聚焦

经典题突破方法 | 统计常见典型考题赏析

经典题突破方法 | 统计常见典型考题赏析

经典题突破方法 | 2023年高考概率经典问题聚焦

经典题突破方法 | 2023年高考概率经典问题聚焦

经典题突破方法 | 概率常见典型考题赏析

经典题突破方法 | 概率常见典型考题赏析

过往期刊

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

中学生数理化·高一数学

猜你喜欢

时代英语·高一

时代英语·初中

高中数理化

发明与创新·上旬刊

语文世界(中学版)

发明与创新·下旬刊

中学生数理化·高二数学

中学生阅读·初中·中考

苏州工业园区教育局电子阅览室

苏州工业园区教育局电子阅览室

新用户注册

注册成功

修改电子邮件

易错题归类剖析 | 立足基础　常考常新

易错题归类剖析 | 立足基础　常考常新