全部分类/
中学教育/
语数外学习·高中版中旬

语数外学习·高中版中旬

2024年01期

《语数外学习》杂志1985年创刊，由湖北第二师范学院主管,湖北第二师范学院主办的优秀教育类期刊。

扫码免费借阅

目录

快速导航

语文 | 谈谈我对高中语文诗词鉴赏单元中学习任务的整合

语文 | 谈谈我对高中语文诗词鉴赏单元中学习任务的整合

人教版高中语文教材针对诗词鉴赏安排了系统的单元学习任务，这些学习任务分散在不同学段的语文教材中，贯穿了高中语文教学的始终。在高三学生复习备考的阶段，为了使诗词鉴赏单元中的学习任务得到更好的落实，我们可以对其进行整合，以帮助学生更好地复习这些知识，提高复习备考的效率。一、整合诗词鉴赏单元中的学习任务诗词鉴赏是语文教材中非常重要的内容，我们可以将诗词鉴赏单元中的学习任务整合起来。人教版高中语文
语文 | 《归园田居（其一）》品读

语文 | 《归园田居（其一）》品读

陶渊明是中国文学史上有名的田园诗人，被后世人誉为“隐逸诗人之宗”“田园诗派之鼻祖”。他历任江州祭酒、镇军参军、彭泽县令等职务，最后却选择遵循自己的本心，辞官归隐，从此不再入仕。《归园田居（其一）》创作于他辞去彭泽县令一职之后，在这首诗歌当中，他不仅描写了如诗如画般的田园风光，而且塑造了率真高洁、热爱自然、崇尚自由的自我形象。下面，笔者就对这首诗作简要的赏析。在诗作的开篇，诗人写道：“少无适俗韵
语文 | 谈谈围绕“传统文化经典研读”任务群开展整本书阅读教学的意义与策略

语文 | 谈谈围绕“传统文化经典研读”任务群开展整本书阅读教学的意义与策略

引导高中生阅读传统文化经典，不仅对培养他们的语文核心素养有重要的意义，而且对其思想品德的提高有极大的作用。因此就显得十分有必要。高中生的学习时间较紧，学习压力较大，我们如何在整本书阅读教学中引导他们充分利用有限的学习时间去阅读整本书呢？这是语文教师需要考虑的问题。本文着重谈谈围绕“传统文化经典研读”任务群开展整本书阅读教学活动的意义与策略。一、开展整本书阅读教学的意义（一）有利于教师从“教
语文 | 浅析我对“生本”教学的几点思考

语文 | 浅析我对“生本”教学的几点思考

素质教育是一种以培养学生的综合素质为中心的教育模式。我们在教学中要遵循“以生为本 ”的原则，以文本为基础对学生进行个性化的指导，以提高他们的阅读能力、思维能力和审美鉴赏能力，营造宽松、民主的教学氛围，培养他们的综合素质。《故都的秋》是新版高中语文教材必修上册第七单元中的第一篇课文。这个单元收录的是写景状物的经典散文。作为语文教师，我们的主要目的是引导学生张开想象的翅膀，感受
语文 | 《立在地球边上放号》的意象之美探析

语文 | 《立在地球边上放号》的意象之美探析

1919年5月4日，“五四运动”爆发，革命的浪潮迅速席卷整个中国。郭沫若受爱国思潮的影响，毅然从日本回国。他在日本横滨，面对无边无际的大海，一时心潮涌动，挥笔写就《立在地球边上放号》。在这首诗作中，诗人以“海的洪涛”为核心意象，描绘了一幅波澜壮阔的图画，展现了“力之美”“力之韵”，将澎湃的激情传递给读者，号召大家向旧的时代、旧的文化、旧的观念发起猛烈的进攻。下面，笔者就简要分析一下《立在地球边上放
语文 | 在单元教学中培养学生语文核心素养的思路与策略

语文 | 在单元教学中培养学生语文核心素养的思路与策略

《普通高中语文课程标准（2017年版2020年修订）》要求语文教师“从祖国语言的特点和高中生学习语文的规律出发，以语文学科核心素养为纲，以学生的语文实践为主线，设计语文学习任务群”。这些学习任务群以任务为导向，以学习项目为载体，对学习的情境、内容、方法和资源进行了一定的整合，可以引导学生在真实的情境中积极地参与实践活动，并培养语文核心素养。学习任务群的出现，意味着开展单元教学是很有必要的。接下来，
语文 | 在“课前演讲”活动中培养学生综合素养的几种举措

语文 | 在“课前演讲”活动中培养学生综合素养的几种举措

“课前演讲”是指在上课前的三到五分钟内，根据不同时段的教学重心，选择适当的演讲话题，组织学生进行演讲的一种活动。如何在激发学生学习兴趣的同时，兼顾其能力与成绩的提高，一直以来都是教育工作者想要努力解决的问题。“课前演讲”有助于提高学生听、说、读、写的能力，增强其分享与合作的意识，丰富其阅历与素材库，树立正确的价值观。对于“如何通过开展‘课前演讲’活动来培养学生的综合素养”这一问题，笔者广泛搜集
语文 | 在语文教学中坚持“五育并举 ”的意义与策略

语文 | 在语文教学中坚持“五育并举 ”的意义与策略

“五育并举”是指通过实施德育、智育、体育、美育、劳育等，促进学生全面发展的教学活动。它体现了现代化国家对人的综合素质的要求。随着素质教育的理念得到更多教师及家长的认同，高中语文学科在促进学生全面发展这一方面的作用也变得更加突出。在高中语文教学中，我们应该尊重学生的主体地位，根据学生的特点因材施教，五育并举。考虑到高中阶段的学生正处于成长的关键时期，身心变化十分迅速，同时面临着高考的压力，对其实施德
语文 | 如何指导学生在文章中展现个人才情

语文 | 如何指导学生在文章中展现个人才情

从近几年的高分考场作文来看，那些展现了个人才情的文章更容易出彩。因此，我们可以顺势而为，有意识地指导学生在文章中展现个人才情。文本就从以下四个方面谈一谈。一、指导学生在文章中表达对材料的理解不少学生喜欢广泛地阅读文化典籍和名人佳作，乐于写读书笔记，积累了较多的文化知识。在指导他们写作文时，我们不妨鼓励他们适当引用或化用古诗词，引用名人言论，以展现较为厚实的知识储备，表达对材料的独到理解。这
语文 | 巧妙切入，点面结合

语文 | 巧妙切入，点面结合

2023年上海高考作文试题在引发学生的思考方面无疑是独具特色的。“一个人乐意去探索陌生世界，仅仅是因为好奇心吗？”这一问让人眼前一亮，引人深思。一个“仅仅”让思维发散开来。那么，同学们在写作时该如何巧妙地切入、深入地展开呢？下面的考场作文也许会给大家带来启示。使命在召唤上海某考生也许你并不起眼，但你却自觉担当，挑战一切不可能，从“微商”起步，一步步走来，率领人们甩掉了“贫穷”的帽子。你
数学 | 例谈两类三角函数问题的解法

数学 | 例谈两类三角函数问题的解法

三角函数是高中数学中的重要模块.三角函数问题的命题形式很多，如求三角函数的单调区间、化简三角函数式、求三角函数的值等.下面主要谈一谈两类三角函数问题的特点以及解法. 一、求三角函数的解析式求三角函数的解析式问题主要有三种命题形式：（1）根据函数的图象求三角函数的解析式；（2）根据三角函数的性质求三角函数的解析式；（3）根据特殊点求三角函数的解析式.这类问题主要考查三角函数的定义域、奇偶性、单
数学 | 求解平面向量的模长问题的三种途径

数学 | 求解平面向量的模长问题的三种途径

若向量为，则向量的模长为l l.平面向量的模长问题主要考查向量的模的公式、向量的数量积、向量运算法则的应用.下面主要探讨一道求解向量的模长问题的三种途径. 题目：已知平面向量，≠，≠，=1，与-的夹角为120∘，则l l的取值范围是. 一、构造几何图形向量兼有“数”与“形”两种身份.因此在解答向量的模长问题时，我们可以从“形”的角度入手，根据题意构造出合适的几何图形，将向量的模长看作几何图
数学 | 如何从不同角度解答一道不等式恒成立问题

数学 | 如何从不同角度解答一道不等式恒成立问题

不等式恒成立问题的常见命题形式有：（1）由恒成立的不等式求参数的取值范围；（2）证明不等式恒成立.不等式恒成立问题具有较强的综合性.这类问题通常会综合考查同学们对导数、函数、不等式、方程等知识的应用情况.下面就一道不等式恒成立问题，谈一谈解答此类问题的方法. 题目：当x>0时，[（a-1）x-1]（x2-ax-1）≥0恒成立，求a的取值范围. 方法一：转化法运用转化法求解不
数学 | 谈谈换元法的应用技巧

数学 | 谈谈换元法的应用技巧

换元法是指通过引入新变量，将其替换某个变量或代数式的方法.换元后，代数式的结构、形式都会有所改变，这便给我们寻找解题思路带来了新的契机.换元包括局部换元、三角换元、均值换元、整体换元.下面结合实例谈一谈换元法的应用技巧. 一、局部换元局部换元是指将代数式的某一部分用一个新元替换.通常可将问题中多次出现的代数式、根号下的式子、分式的分母、绝对值内部的式子用新元替换，便可通过局部换元，将代数式简
数学 | 三角函数周期的三种求法

数学 | 三角函数周期的三种求法

周期性是三角函数的一个重要性质.求解三角函数周期问题，通常需仔细研究函数的图象或解析式.下面，笔者结合实例谈一谈求三角函数周期的几种方法. 一、定义法对于函数y=f（x），若存在一个不为零的常数T，使得当x取定义域中的每个值时，都有f（x+T）=f（x），则常数T是函数y=f（x）的周期，此时函数y=f（x）为周期函数.运用定义法求三角函数的周期，需通过恒等变换，建立f（x+T）与f（x）之
数学 | 由一道题谈求解多元最值问题的措施

数学 | 由一道题谈求解多元最值问题的措施

多元最值问题中涉及了多个变量，我们往往需根据变量之间的关系或限制条件来求某个代数式的最值.如何处理好变量之间的关系，将目标式进行合理的变形是解题的关键.下面结合一道例题，谈一谈求解多元最值问题的几种措施. 题目：已知 a，b，m，n 均为正数，且 a + b = 1，mn = 2 ，则（am + bn）（bm + an）的最小值是________. 题目中涉及了四个变量 a、b、
数学 | 求解双变量问题的几个“妙招”

数学 | 求解双变量问题的几个“妙招”

双变量问题通常较为复杂，常与函数、导数、方程、不等式等知识相结合.这类问题的难度较大，对同学们的分析、运算、抽象思维能力有较高的要求.解答双变量问题的一般思路是将双变量问题转化为单变量问题来求解，那么如何进行转化呢？主要有以下三个“妙招”. 一、构造同构式通过变形，有些不等式或等式两侧的式子可化为结构相同、形式相似的式子，即同构式，那么就可以根据同构式的结构特征构造出相应的函数模型.这样便可
数学 | 判断函数奇偶性的三种路径

数学 | 判断函数奇偶性的三种路径

奇偶性是函数的一种重要性质.判断函数奇偶性问题的难度不大，同学们需灵活运用奇函数和偶函数的定义，结合函数的定义域、图象、性质等进行判断.判断函数的奇偶性主要有三种路径：利用定义法、图象法以及性质法，下面将结合实例作详细的介绍. 一、利用定义法定义法是指根据函数奇偶性的定义来进行判断，该方法是判断函数奇偶性的重要方法.我们知道，具有奇偶性的函数关于原点对称，因此判断函数的奇偶性，需首先判断函数
数学 | 巧用参数方程，妙解圆锥曲线题

数学 | 巧用参数方程，妙解圆锥曲线题

直线与圆锥曲线都有相应的参数方程.在解答圆锥曲线问题时，灵活运用参数方程，不但能够降低解题的难度，还可以提高解题的效率.下面结合实例，谈一谈如何巧妙运用直线、椭圆、双曲线的参数方程解答圆锥曲线问题. 一、巧用直线的参数方程解题若直线 l 过点（x0，y0），且倾角为 θ ，则其参数方程为 ì í î x = x0 + t cos θ， y = y0 + tsin θ，t 为参数
数学 | 选用合适的方法，提升解答偶函数不等式问题的效率

数学 | 选用合适的方法，提升解答偶函数不等式问题的效率

函数不等式问题比较常见，其中偶函数不等式问题主要考查基本初等函数的定义、性质，以及偶函数的定义、图象的应用.笔者对一道偶函数不等式问题的解法进行了深入的探讨，并对这一类问题及其解法进行归纳总结. 题目：一、分类讨论法对于偶函数而言，在 y 轴左右两侧的函数图象关于 y 轴对称，因而两侧的函数单调性往往不相同，那么就需分 x < 0 和 x > 0 两种情况进行分类
数学 | 对一道最值问题的解法的探究

数学 | 对一道最值问题的解法的探究

最值问题比较常见.解答最值问题通常有多种不同的方法和思路.本文以2023年高考乙卷文科单选题的第11题为例，谈一谈最值问题的解法，以供大家参考. 题目：已知实数x，y满足x2+y2-4x-2y-4=0，则x-y的最大值是（）. A.1+B.4 C.1+3 D.7 该题的难度不大，要求x-y的最大值，需重点研究已知关系式x2+y2-4x-2y-4=0，将其作为约束x、y的条件，来寻找解题的思路
数学 | 例谈用同构法解答函数不等式问题的步骤

数学 | 例谈用同构法解答函数不等式问题的步骤

同构法在解答函数、方程、不等式等问题中应用广泛.而运用同构法解题的关键是构造出同构式.同构式是指结构相同，形式相似的式子.对于较为复杂的函数问题，如函数最值问题、函数不等式问题、函数单调性问题，利用同构法求解，可使问题快速得解. 运用同构法解答函数不等式分以下5个步骤： 1.将不等式进行适当的变形，通过移项、合并同类项、拆项、添项、凑系数、取倒数、取对数等方式，使得不等式两侧的式子为同构式；
数学 | 合理构造辅助数列，快速求数列的通项公式

数学 | 合理构造辅助数列，快速求数列的通项公式

求数列的通项公式问题比较常见，解答这类问题需将已知关系式或递推关系式进行合理的变形，以构造出辅助数列，通过求辅助数列的通项公式求得问题的答案.那么如何构造辅助数列呢？主要有两种方法：构造等差数列或等比数列. 一、构造等差数列我们知道，若数列的前后两项的差为一个常数，则该数列为等差数列.由复杂的递推式求数列的通项公式时，若能将递推式变形为an-an-1=f（n）的形式，就可将数列{an}看作等
数学 | 怎样解答三角函数最值问题

数学 | 怎样解答三角函数最值问题

三角函数最值问题通常综合考查三角函数的基本公式、性质、图象的应用.这类问题的命题形式多样，解法也各不相同.下面结合一道例题，谈一谈解答三角函数最值问题的几种方法. 题目：已知+=1，求+的最小值. 解法一：柯西不等式法柯西不等式是解答最值问题常用的方法.柯西不等式即：对于实数a，b，c，d，（a2+b2）（c2+d2）≥（ac+bd）2，当且仅当ad=bc时取等号.运用柯西不等式解题，需对
数学 | 《等差数列及其前n项和》专题训练

数学 | 《等差数列及其前n项和》专题训练

一、单选题二、多选题三、填空题四、解答题参考答案与解析一、单选题二、多选题三、填空题四、解答题
英语 | 在单元教学中培养学生文化意识的策略

英语 | 在单元教学中培养学生文化意识的策略

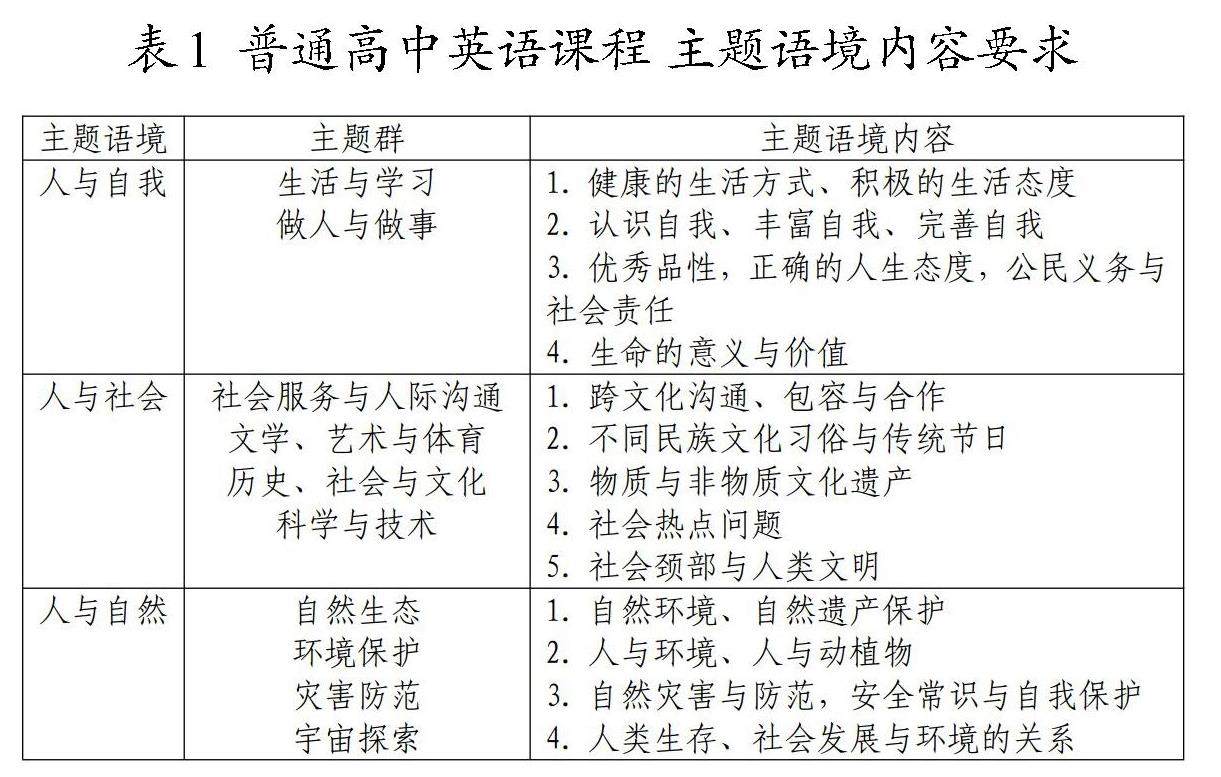
文化意识是指学生对中外文化的理解以及对优秀文化的鉴赏，体现在跨文化认知、态度和行为选择等方面。单元教学中文化意识的培养体现出进阶性和整体性的特点。进阶性体现在从知识获取到品格塑造的逻辑路径，历经认知、态度、行为等三个阶段。基于此，文章以译林版高中英语选择性必修一Unit 3 The art of painting的教学为例，剖析开展教学的方法，旨在提升学生的文化意识。一、补充文化知识，形成文化
英语 | 聚焦主题语境，开展高中英语阅读教学

英语 | 聚焦主题语境，开展高中英语阅读教学

英语阅读是学生搜集文本信息、发展认知思维、获得审美体验的一种学习活动，也是对阅读文本进行重新加工的个性化活动。阅读的目的，不仅仅是学习文本思想主旨、语言特征和表达风格，还要理解文本中的文化语境、情境语境及交际语境。所以，英语阅读教学应该在一定的主题语境下开展，让学生在不同类型的语篇和语境中了解语言文化、深化理解语言、探究语言特征、汲取语言精华，从而帮助学生在英语阅读的过程中培养语言素养和文化素养，
英语 | 在高中英语教学中应用思维可视化工具的方法

英语 | 在高中英语教学中应用思维可视化工具的方法

思维品质是高中英语学科核心素养的构成要素之一。它的发展有利于提升学生分析和解决问题的能力。培养学生的思维品质就是在践行英语学科的育人价值，体现出英语学科是人文性和实用性的统一体。人的思维本身就是隐形的、独特的，将思维变得可视化的过程就是将思维进行显性的展示，结构性、全程性地呈现出来。概念图（concept map）、思维导图（mind map）和思维地图（thinking map）是三种最常用的思
英语 | 浅析2023年高考题中主旨大意阅读题的命题特点

英语 | 浅析2023年高考题中主旨大意阅读题的命题特点

主旨大意题着重考查学生对文章信息提炼加工的能力。从内容上可以分为选择最佳标题类、总结大意类、目的类等。不同的类别采取的解题方法也不同。下面以2023年高考阅读题为例，对其中两种考查类型进行解读，旨在对学生有所助力。一、选择最佳标题类此类题目通常是以要求学生为文章选一个最适合的标题的形式出现，需要学生对整个语篇的核心要义进行提炼与概括，并对选项中的措辞进行对比分析，从中选出囊括全文主旨内容的
英语 | 例谈解答读后续写题的几个步骤

英语 | 例谈解答读后续写题的几个步骤

读后续写题既考查阅读能力又考查写作能力，其解题的关键是要明晰如何“读”，怎样“写”。下面笔者将以2023年浙江卷（1月）读后续写题为例，剖析“读”的内容，“写”的要点，旨在帮助学生掌握读后续写的技巧，提升续写水平，从而获取高分。一、读懂材料大意，理清行文脉络续写前，读懂所给的材料是关键。此处的“读”包括读首句、要素、语篇结构、情感变化、体裁等内容。对阅读材料进行解读，理清故事中的主要人物以
英语 | 根据设空位置，寻找解答2023年高考题中“七选五”阅读题的突破口

英语 | 根据设空位置，寻找解答2023年高考题中“七选五”阅读题的突破口

“七选五”阅读题按照设空位置分为标题、段首、段中、段尾等四类。不同的设空位置其考查方向亦不同，但均是对语篇整体内容以及上下文逻辑关系等的考查。下面以2023年的高考题为例，按照设空位置剖析解题策略，旨在帮助学生提升解题技巧，获取高分。一、标题处设空标题处设空通常是考查学生对其所在段落的大意进行概括提炼的能力，其形式一般都会与语篇中的其他小标题在风格上具有一致性。解题时，学生通过概括段落大意
英语 | 活用构词法，巧记英语单词

英语 | 活用构词法，巧记英语单词

通过学习构词法，学生可以将复杂的单词分解成相对简单的几个部分，从而更容易去记忆和理解。下面，让我们一起来看看如何活用构词法，巧记英语单词吧！一、转化法有些单词是通过将一种词性转化为另一种词性形成的，而这种转化不会改变单词的词形，这就是所谓的转化法。简而言之，转化法就是某些单词具有两种以上的词性，比如名词可转化为动词、动词可转化为名词、形容词可转化为副词、名词可转化为形容词等等。通过应用转化
英语 | 定语从句的常见考点归纳

英语 | 定语从句的常见考点归纳

定语从句是英语语法中的一个重要部分，也是历年高考考查的重点之一。本文结合高考真题探讨了定语从句的常见考点。考点一、考查关系代词的用法关系代词在从句中代替被修饰的名词或代词，位于被修饰的词之后，可在从句中作宾语、主语等句子成分。常见的关系代词有who，whom，whose，which，that等。注意：先行词指物且在从句中作主语时，关系代词应用which或that，二者在一般情况下可互换使用
英语 | 怎样引导学生进行课后小结

英语 | 怎样引导学生进行课后小结

维茨金曾说：“我们能成为顶尖选手并没有什么秘诀，而是对可能是基本技能的东西有更深刻的理解。”教师在高中英语课堂上传授的基础知识数量多、内容杂，而学生要想掌握这些知识，需要花费大量时间和精力，在课下通过晨读、晚读和做练习重复记忆及巩固，学习的效果却不尽如人意。要想改变这一状况，教师不妨留出课堂最后的五分钟时间，趁热打铁指导学生进行课后小结，从而帮助学生发现知识误区，检验学生是否能将课堂上所学的新知识

过往期刊

更多

猜你喜欢

苏州工业园区教育局电子阅览室