目录
快速导航-

艺术视角 | 小舟从此逝,江海寄余生
艺术视角 | 小舟从此逝,江海寄余生
-
拓展阅读 | 统编语文教材九(上)第三单元拓展阅读
拓展阅读 | 统编语文教材九(上)第三单元拓展阅读
-
拓展阅读 | 喜雨亭记
拓展阅读 | 喜雨亭记
-
拓展阅读 | 峡江寺飞泉亭记
拓展阅读 | 峡江寺飞泉亭记
-
拓展阅读 | 统编语文教材九(上)第四单元拓展阅读
拓展阅读 | 统编语文教材九(上)第四单元拓展阅读
-
拓展阅读 | 小径分岔的花园
拓展阅读 | 小径分岔的花园
-
拓展阅读 | 官场现形记(节选)
拓展阅读 | 官场现形记(节选)
-
作文升格 | 紧扣论点 言必有据
作文升格 | 紧扣论点 言必有据
-
作文升格 | 留干删枝成一文
作文升格 | 留干删枝成一文
-
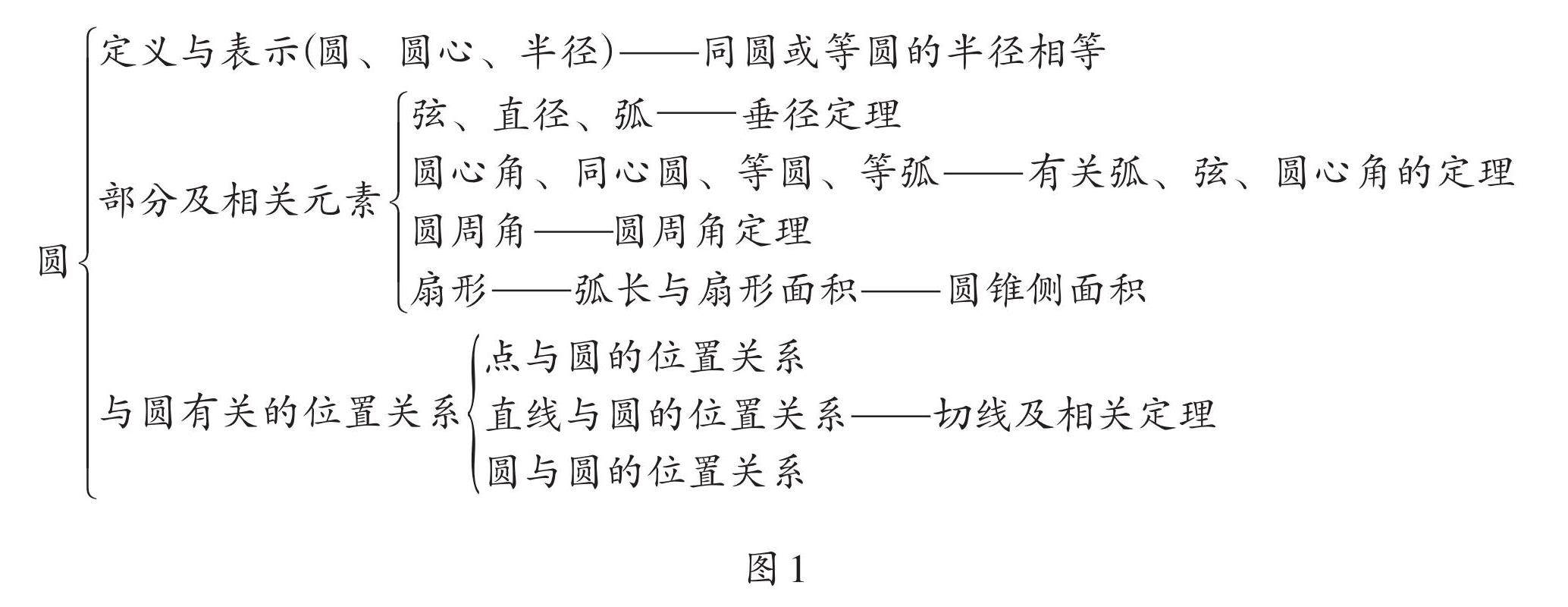
整体解读 | 紧扣“联系”,提高学习效率
整体解读 | 紧扣“联系”,提高学习效率
-
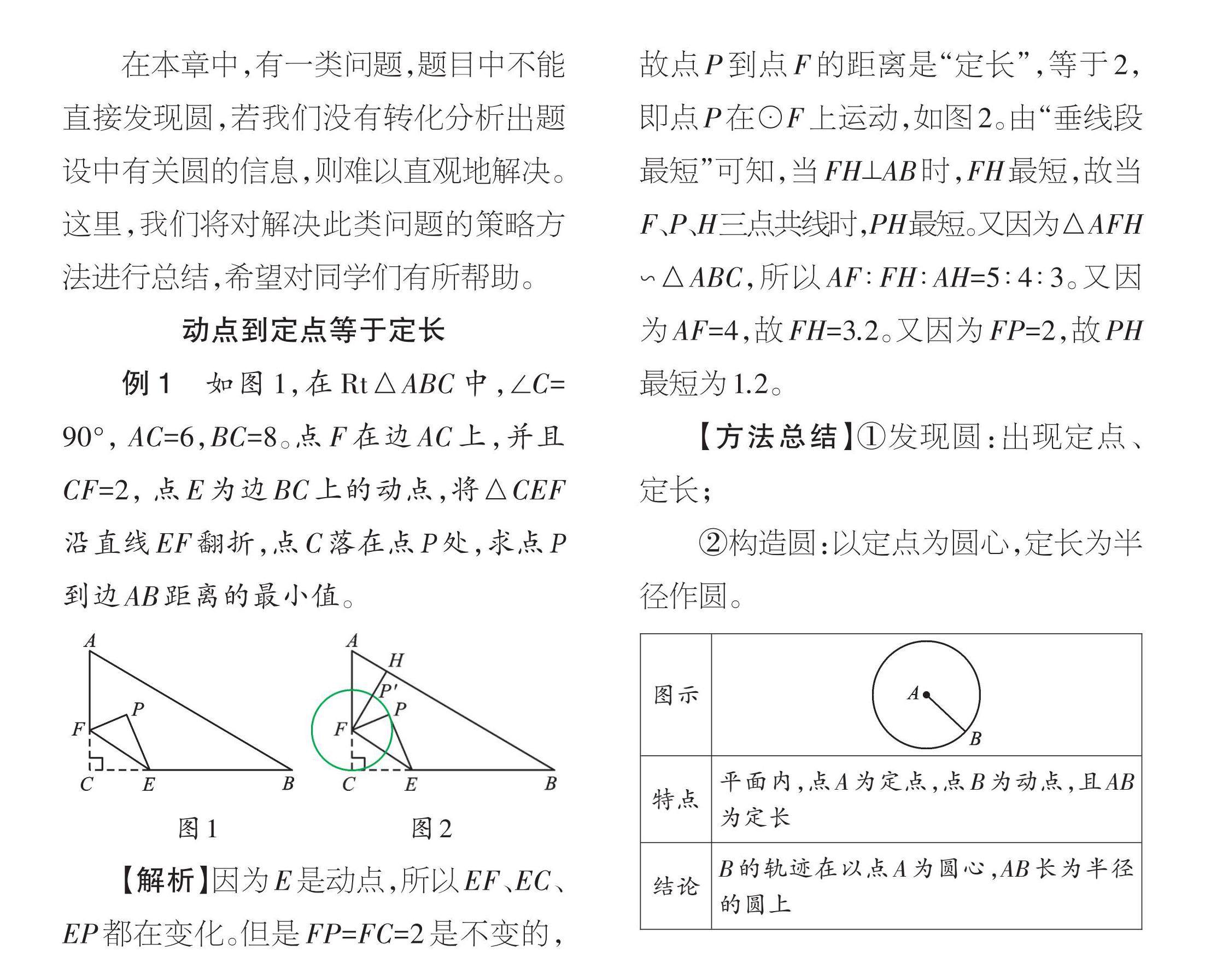
策略方法 | 循规为圆,以智为径
策略方法 | 循规为圆,以智为径
-

纠错解析 | 他山之“圆”,可以攻玉
纠错解析 | 他山之“圆”,可以攻玉
-

例题延展 | 深究教材例题,提高解决问题能力
例题延展 | 深究教材例题,提高解决问题能力
-
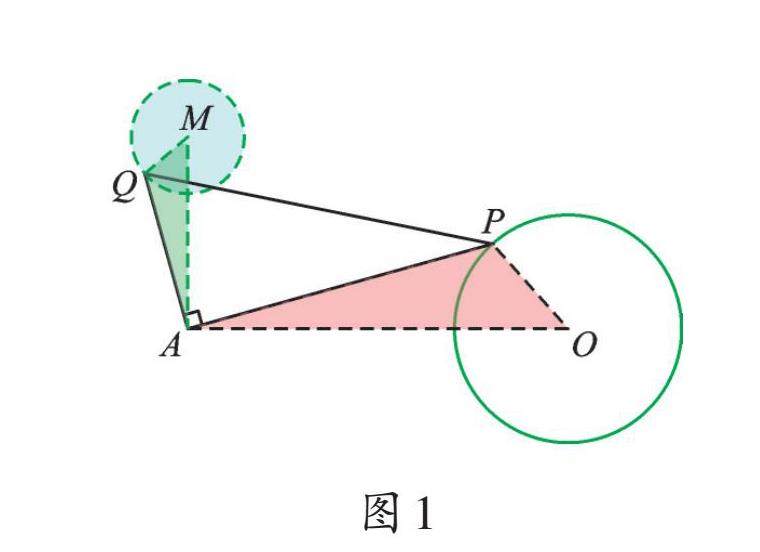
一通百通 | “两动三定”想“瓜豆”,隐圆最值不用愁
一通百通 | “两动三定”想“瓜豆”,隐圆最值不用愁
-

中考链接 | 巧添辅助线,妙解“圆”问题
中考链接 | 巧添辅助线,妙解“圆”问题
-
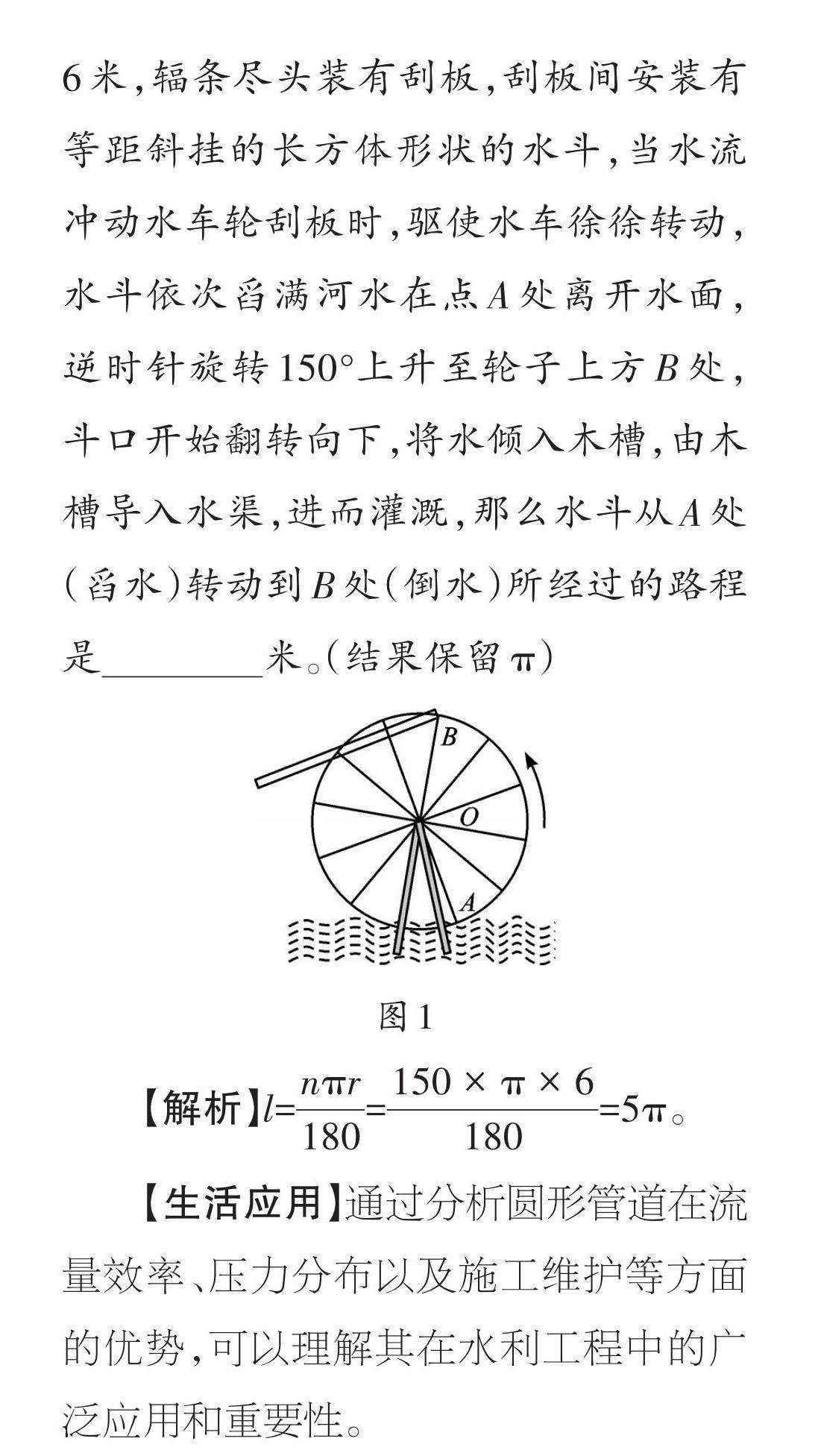
生活数学 | 圆的数学之美:从水利工程到建筑设计
生活数学 | 圆的数学之美:从水利工程到建筑设计
-
动手做数学 | 莱洛三角形与圆
动手做数学 | 莱洛三角形与圆
-
英语读写 | Teenage problems
英语读写 | Teenage problems
-
英语读写 | Growing up
英语读写 | Growing up
-

校园里的红色印迹 | 江苏省启东市东南初级中学:追寻红色记忆,弘扬抗大精神
校园里的红色印迹 | 江苏省启东市东南初级中学:追寻红色记忆,弘扬抗大精神





















 登录
登录