目录
快速导航-
卷首语 | 让人生尽享数学之美
卷首语 | 让人生尽享数学之美
-
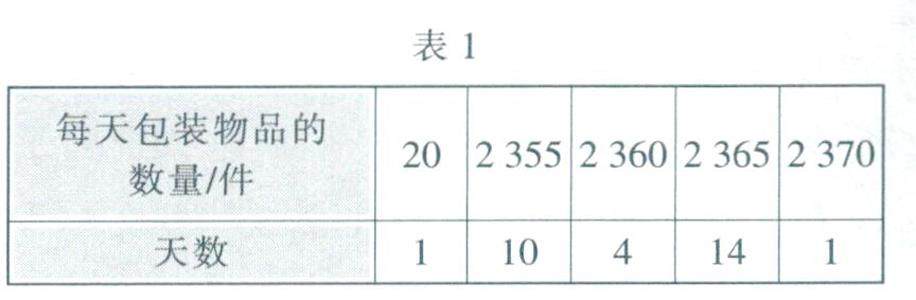
数学之基 | 常用的几个数据代表
数学之基 | 常用的几个数据代表
-
数学之基 | 趣谈数据的“三个代表”
数学之基 | 趣谈数据的“三个代表”
-

数学之基 | 分析数据离不开数学思想
数学之基 | 分析数据离不开数学思想
-

数学之基 | 聚焦“三数”问题 辨析“三数”特征
数学之基 | 聚焦“三数”问题 辨析“三数”特征
-
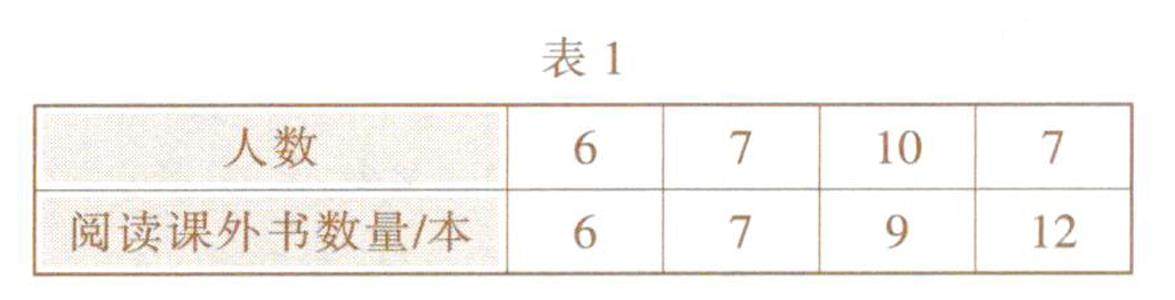
数学之基 | “三数一差”与图表同行
数学之基 | “三数一差”与图表同行
-
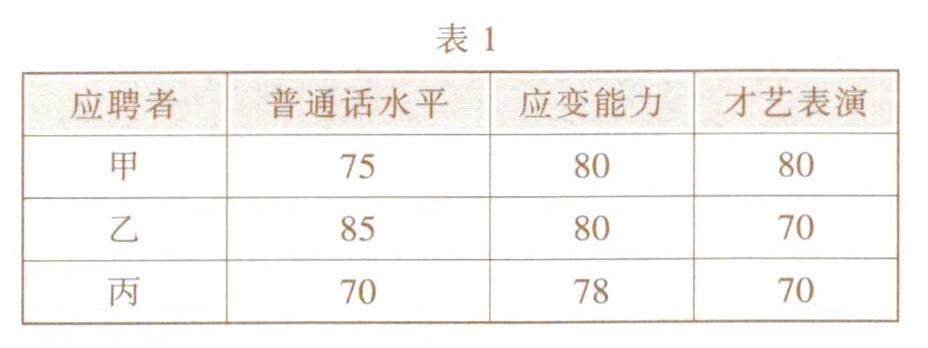
数学之基 | 用好手中的“权”
数学之基 | 用好手中的“权”
-
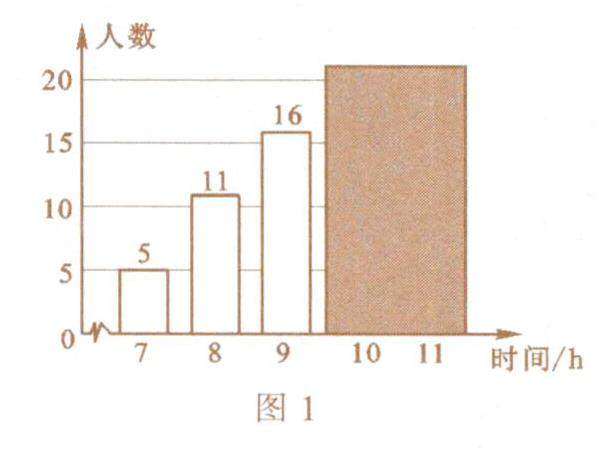
数学之基 | 数据分析 创新中考
数学之基 | 数据分析 创新中考
-

数学之基 | 巧变方差公式 妙解数学难题
数学之基 | 巧变方差公式 妙解数学难题
-
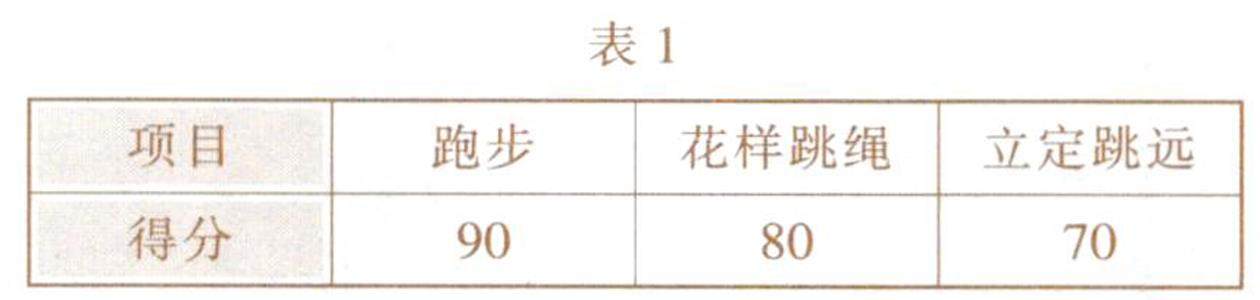
数学之基 | “数据的分析”易错点剖析
数学之基 | “数据的分析”易错点剖析
-
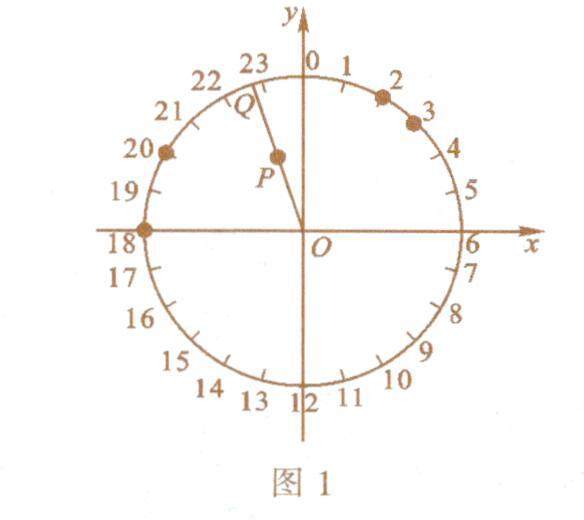
数学之趣 | 平均几点钟怎么求
数学之趣 | 平均几点钟怎么求
-
数学之趣 | 自律带来自由
数学之趣 | 自律带来自由
-
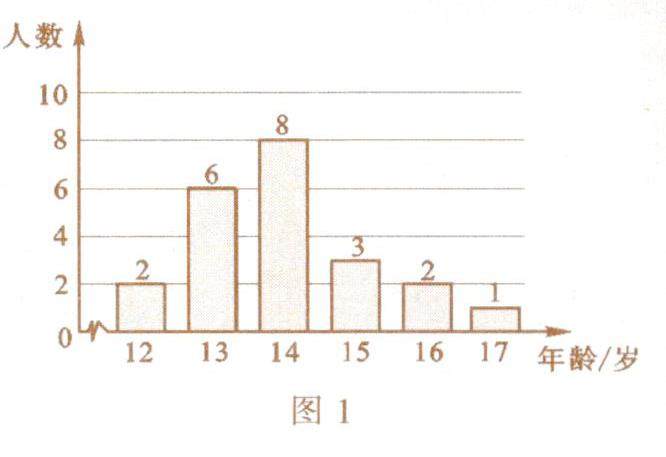
数学之趣 | 数学潜能知识竞赛
数学之趣 | 数学潜能知识竞赛
-
数学之趣 | 当当闯关记
数学之趣 | 当当闯关记
-
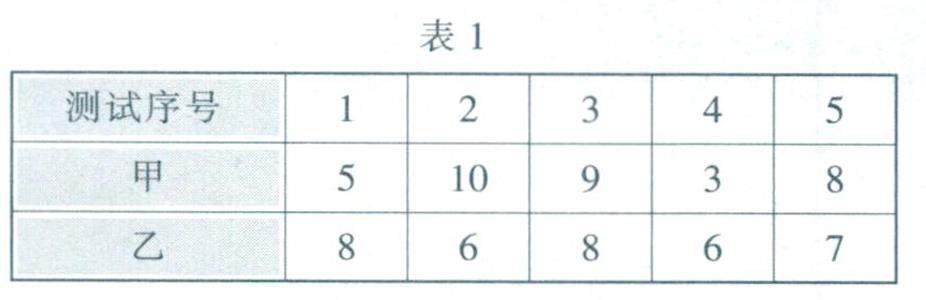
数学之用 | “数据的分析”新题总动员
数学之用 | “数据的分析”新题总动员
-
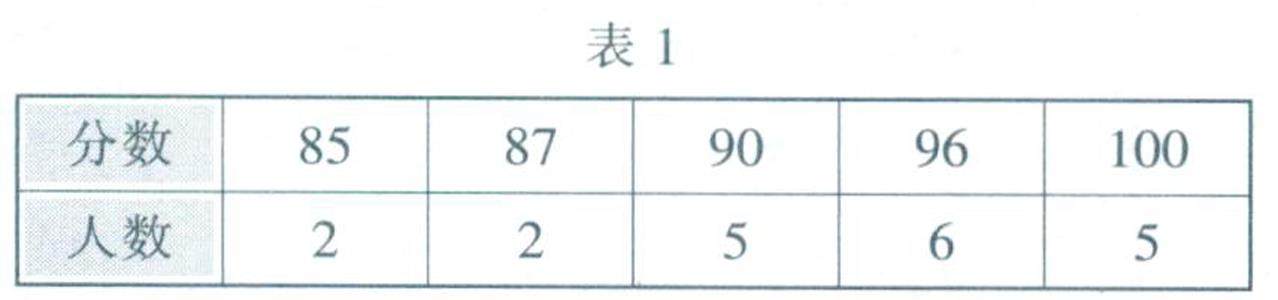
数学之用 | “数据的集中趋势”知识演练
数学之用 | “数据的集中趋势”知识演练
-
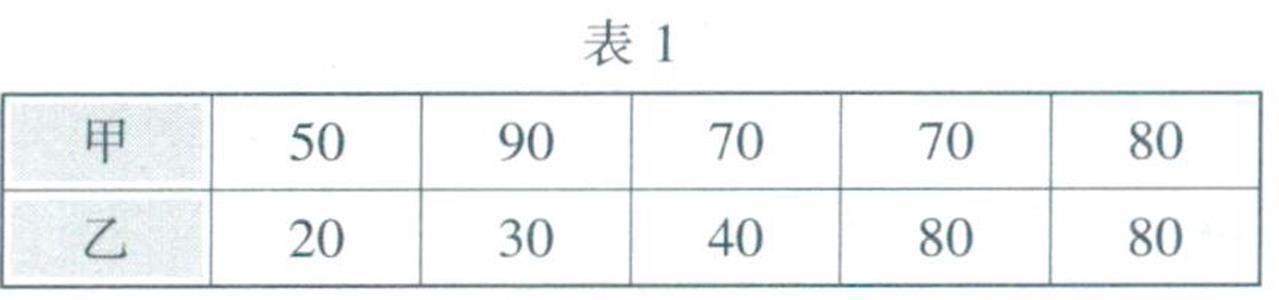
数学之用 | “数据的波动程度”专项突破
数学之用 | “数据的波动程度”专项突破
-

数学之用 | “数据的分析”易错题专练
数学之用 | “数据的分析”易错题专练
-
数学之用 | 本期练习类题目参考答案及提示
数学之用 | 本期练习类题目参考答案及提示




















 登录
登录