目录
快速导航-
卷首语 | 为学应须毕生力,攀登贵在少年时
卷首语 | 为学应须毕生力,攀登贵在少年时
-

数学之基 | 拓宽对函数的认识
数学之基 | 拓宽对函数的认识
-
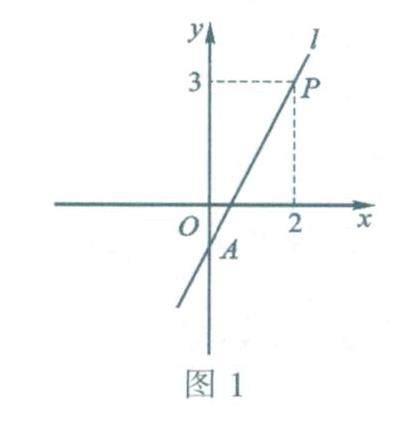
数学之基 | 紧抓特征 触类旁通
数学之基 | 紧抓特征 触类旁通
-
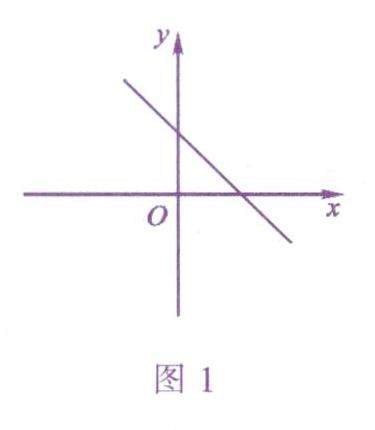
数学之基 | 一次函数增减性的应用
数学之基 | 一次函数增减性的应用
-
数学之基 | 一次函数实际应用之“最”
数学之基 | 一次函数实际应用之“最”
-
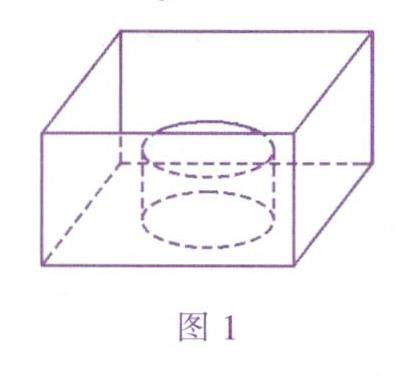
数学之基 | 观图象 获信息
数学之基 | 观图象 获信息
-

数学之基 | 一次函数联姻几何图形
数学之基 | 一次函数联姻几何图形
-
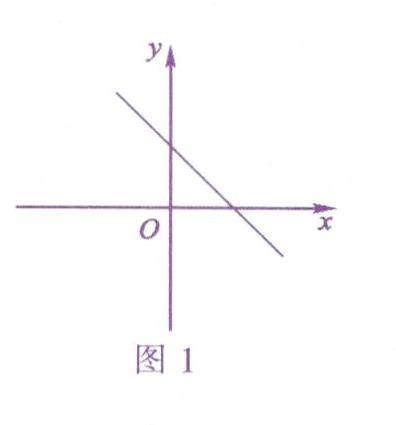
数学之基 | 一次函数错解“诊疗室”
数学之基 | 一次函数错解“诊疗室”
-
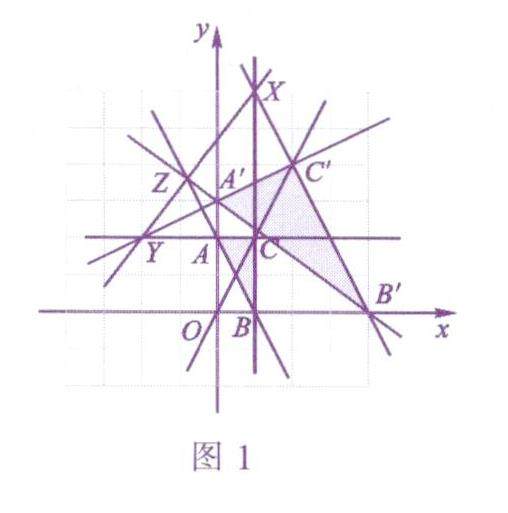
数学之趣 | 笛莎格定理
数学之趣 | 笛莎格定理
-
数学之趣 | 如何背着“壳”前行
数学之趣 | 如何背着“壳”前行
-
数学之趣 | 当当闯关记
数学之趣 | 当当闯关记
-
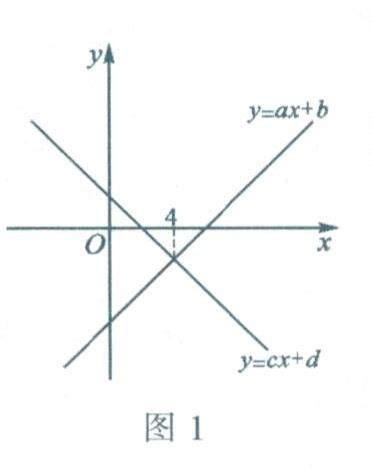
数学之趣 | 数学潜能知识竞赛
数学之趣 | 数学潜能知识竞赛
-
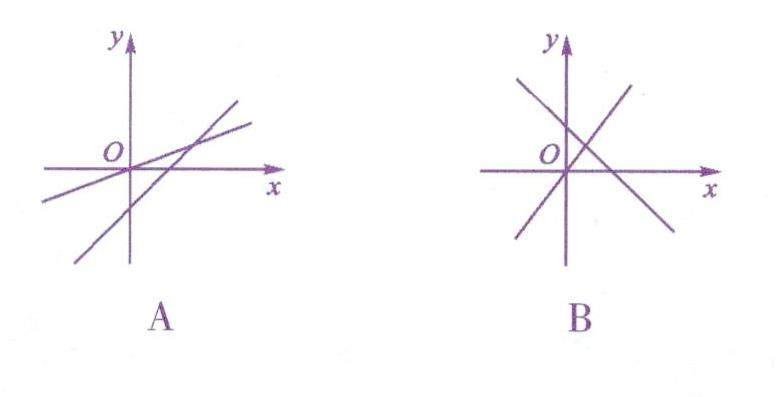
数学之用 | “一次函数”新题总动员
数学之用 | “一次函数”新题总动员
-
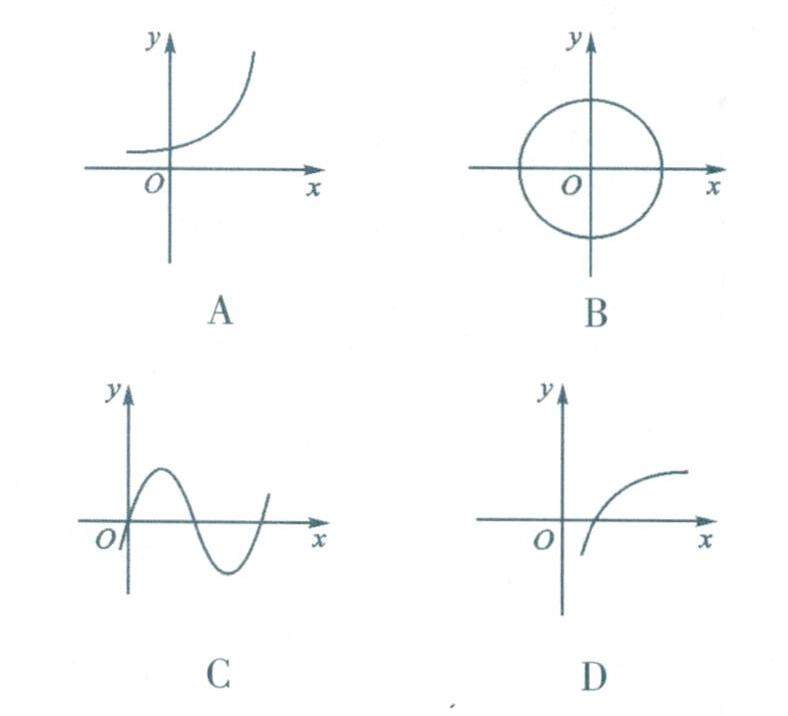
数学之用 | “函数及其图象”夯基础
数学之用 | “函数及其图象”夯基础
-
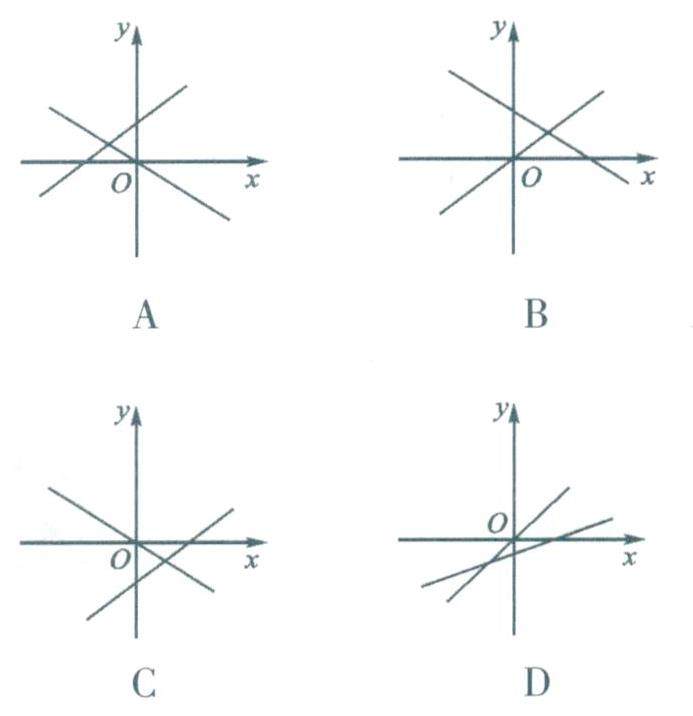
数学之用 | “一次函数的图象与性质”划重点
数学之用 | “一次函数的图象与性质”划重点
-
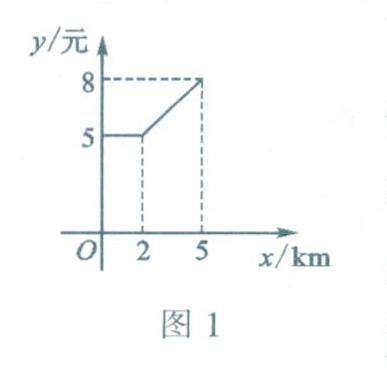
数学之用 | “一次函数的应用”练通关
数学之用 | “一次函数的应用”练通关
-
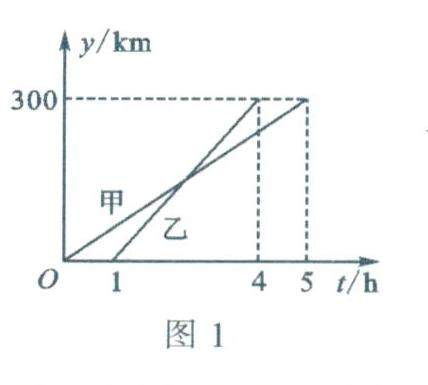
数学之用 | “一次函数”易错题专练
数学之用 | “一次函数”易错题专练
-

数学之用 | 本期练习类题目参考答案及提示
数学之用 | 本期练习类题目参考答案及提示




















 登录
登录